「 統計学話 」一覧

品質特性値とは品質の評価を数値化することです。 品質はできるかぎり数値化して評価するようにすべきです。数値化しないで人の感覚で判断を...

試合をする人やチームの数をN とすると、1試合ずつの総当たり戦をしたときの試合数は、次の式で計算することができます。 N（N－1）÷...

試合をする人やチームの数をN とすると、1試合ずつの総当たり戦をしたときの試合数は、次の式で計算することができます。 N（N－1）÷...

試合をする人やチームの数をN とすると、1試合ずつの総当たり戦をしたときの試合数は、次の式で計算することができます。 N（N－1）÷...

試合をする人やチームの数をN とすると、1試合ずつの総当たり戦をしたときの試合数は、次の式で計算することができます。 N（N－1）÷...

傾向変動とは、時系列データの変動のなかで長期的な時間の経過とともに増加をする変化、または減少する変化のことです。トレンドともいいます。 ...

時系列データのなかでトレンド・季節変動・循環変動では説明できない変動のことを不規則変動といいます。 微細な変動もありますし、異常な突...

循環変動は、長い期間のなかである周期性をもって現れる変動のことです。経済が好景気になったり不景気になったりするのは循環変動といえます。 ...

季節変動とは、時系列データの変動のなかで季節的な要因による変動です。毎年1年のなかでほぼ同じ形で表れる変動であり、12か月で一周します。 ...

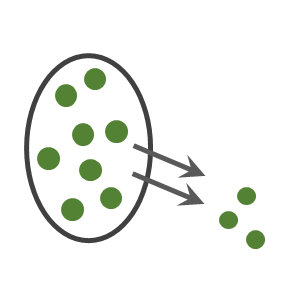
系統サンプリングは一定の間隔でサンプルをとる方法です。系統抽出法ともいいます。 たとえば工場内で製造している製品がコンベアの上などを...

層別サンプリングとは、母集団をいくつかの層に分けてその中からランダムサンプリングする方法です。 母集団の中に構成がある場合には、単純...

集落サンプリングとは、まず母集団をいくつかのグループに分け、その部分をランダムに選び出します。その選んだグループを全て調査対象とする方法で...

多段サンプリングとは、第一段階として母集団をいくつかに区分けしてブロックを作ります。そのブロックをランダムに選び出し、さらにその中からラン...

単純ランダムサンプリングとは、無作為に標本を選ぶ方法です。無作為抽出ともいいます。 “無作為に選ぶ”とは人の意思の影響がなく偶然によ...

尺度とは、ものごとを評価したり判断したりする時の、ものさし・基準のことです。名義尺度・順序尺度・間隔尺度・比率尺度があります。 比率...

尺度とは、ものごとを評価したり判断したりする時の、ものさし・基準のことです。名義尺度・順序尺度・間隔尺度・比率尺度があります。 間隔...

尺度とは、ものごとを評価したり判断したりする時の、ものさし・基準のことです。名義尺度・順序尺度・間隔尺度・比率尺度があります。 順序...

尺度とは、ものごとを評価したり判断したりする時の、ものさし・基準のことです。名義尺度・順序尺度・間隔尺度・比率尺度があります。 名義...

人生ではじめて宝くじを買ったときのこと。 その宝くじ売り場の看板には、「出ました！大当たり！2等・5500万円」と大々的に宣伝文句が...

他の人がつくった分析結果を見るときには、なんらかのバイアスにかかっていないかどうか注意して見る必要があります。もしバイアスのある分析結果で...

19世紀から20世紀にかけてのフランスに、ポアンカレという数学者がいて、統計学を使ってパン屋の不正を見抜いた逸話があります。 パンの...

「ガーベッジ・イン、ガーベッジ・アウト」 「ゴミを入れれば、ゴミが出てくる」 このようなデータ分析に関連した格言があります。英...

統計学は、今あるデータを用いて、少ないデータでもとの調査対象の特性を推測したり、AかBどちらの案がよいのかを判断したり、将来がどうなるか計...

統計学を仕事に活用して役立てることができるかどうか、これは、職場の環境による部分もあるのではないかと思います。 統計学的な説明はわか...

確率の基本的な公理には、 どのような事象でも確率は0 から1 の間になる。すべての事象の確率は1 となる があります。 ...

仕事をしていれば、様々な問題にぶつかります。 その問題を解決しなければならないが、原因の詳細がいまいちわからない。だから問題解決でき...

小さな確率のことであっても、広い範囲でみればしばしば発生するのは当たりまえと認識しまよう。自分にも起こるとは限らない。この記事で言いたいこ...

大数の法則とは、試行の回数を増やしていくほど、結果は本来の確率に限りなく近づいていく法則です。 コイン投げの結果は本来の確率に収束す...