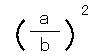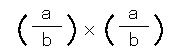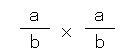An
これは、Aをn乗することをあらわしています。Aの右肩に乗ったnは指数と呼ばれ、Aを何乗するかを示すものです。次のような関数があったとしましょう。
Y = X2
指数とは特定の数を何乗かすることでして、指数を用いた関数のことを、指数関数と呼びます。Xが決まればYも決まります。xは3 であれば、yは9 となります。
指数法則
指数の便利なところは、
- 掛け算を足し算で考えることができる
- 割り算を引き算で考えることができる
- 何乗するのかの計算を掛け算で考えることができる
- ルートの計算を割り算で考えることができる
などです。
- a ≠ 0
- m とn が正の整数
であるとき、成り立つ法則を説明していきます。
同じ数を累乗したものの掛け算は、指数を足せばよい
累乗とは、同じ数を順に掛け合わせることです。同じ数を累乗したもの同士の掛け算は、指数を足し算して計算することができます。
am × an = am+n
たとえば、
23 × 23 × 23
を掛け算して計算すると、
23 × 23 × 23
=8×8×8
=512
となります。指数の足し算をすると、
23 × 23 × 23
= 23+3+3
= 29
となります。
29 = 512
ですから、同じ結果となります。
同じ数を累乗したものの割り算は、指数を引けばよい
同じ数を累乗したものの割り算は、指数を引くだけで計算ができてしまいます。
am ÷ an = am-n
累乗のとても大きな数値で考えてみましょう。
106 ÷ 103
= 1,000,000 ÷ 1,000
= 1,000
となるのですが、指数をそのまま引けば計算ができてしまいます。
106 ÷ 103
= 106-3
= 103
となります。6個の0 から 3個の0を引いた形になります。
累乗したものの累乗は、指数を掛け算すればよい
累乗したものの累乗は、指数を掛け算すれば計算することができます。
(am )n = am×n
(103 )3 = 1,000 × 1,000 × 1,000
= 1,000,000,000
となります。これを指数をつかってあらわすと、109 です。このように桁数を多くして扱わなくても、指数をそのまま掛け算すれば計算ができてしまいます。
(103 )3 = 103×3
= 109
となります。
掛け算を先にしても、別々に累乗を先にしてもよい
掛け算したものを累乗する場合は、別々に累乗をして、そのあとに掛け算をしても計算することができます。
(a × b)n = an × bn
となります。
(2×3)3
=63
=216
ですけれども、別々に累乗して計算しても、
(2×3)3
=23 × 33
=8 × 27
=216
となります。このルールは、数式を整理するときなどに役立ちます。
ちなみに、
(2+3)3
と、( )の中が足し算の場合はこのルールは成り立ちません。
(2+3)3 ≠ 23 + 33
計算してみると
(2+3)3
= 53
= 125
となり、216 とはなりません。同じように( )の中が引き算のときも成り立ちません。
(2-3)3 ≠ 23 - 33
-13 ≠ 8 - 27
-1 ≠ -19
割り算を先にしても、別々に累乗を先にしてもよい
割り算したものを累乗する場合は、別々に累乗をして、そのあとに割り算をしても計算することができます。
(a ÷ b)n = an ÷ bn
(a ÷ b)2 を紐解いていくと、
となります。
(a ÷ b)2 = a2 ÷ b2
が成り立ちます。a=36、b=6 としたら、式の左辺は、
(36 ÷ 6)2
= 62
= 36
となります。
右辺でも、
362 ÷ 62
=1296 ÷ 6
=36
となります。
0乗は1になる
a0 = 1
ある数の0 乗は、1 であると定義されています。
50 = 1
100 = 1
となります。どんな数であっても、肩に0 が乗っかれば、1 となるのです。
ある数をマイナス何乗かすると、そのある数乗分の1 となる
ある数をマイナス何乗かすると、「その数乗分の1」とおなじ意味になります。
a-n = 1 / an
10に指数をつけて考えてみると、
10-1 = 1 / 101
10-2 = 1 / 102
10-3 = 1 / 103
こういった具合です。
106 ÷ 107
= 1,000,000 ÷ 10,000,000
= 1 ÷ 10
となりますね。同じ数を累乗したものの割り算は、指数を引くことができるという法則で考えると、
106 ÷ 107
= 106-7
= 10-1
となり、
10-1 = 1/101 = 1/10
であることがわかります。
また、ある数の逆数も、もとの数のマイナス1乗であると考えることができます。
a × ( 1 /a)= 1
aの逆数は、1/aですね。
a × a-1
=a ×( 1 /a1 )
=a ×( 1 /a )
= 1
まとめ
もう一度ざっと指数法則を振り返ります。
・同じ数を累乗したものの掛け算は、指数を足せばよい
am × an = am+n
・同じ数を累乗したものの割り算は、指数を引けばよい
am ÷ an = am-n
・累乗したものの累乗は、指数を掛け算すればよい
(am )n = am×n
・掛け算を先にしても、別々に累乗を先にしてもよい
(a × b)n = an × bn
・割り算を先にしても、別々に累乗を先にしてもよい
(a ÷ b)n = an ÷ bn
・0乗は1になる
a0 = 1
・ある数をマイナス何乗かすると、そのある数乗分の1 となる
a-n = 1 / an
指数の法則は、数式をより簡単に計算したり、整理したりするときに役立ちます。統計学を学んでいて出会う数式やその説明を理解するときにも役立つ場面があります。