エクセルには、標準偏差を計算する関数があります。STDEV.PとSTDEV.Sの2つです。
両方とも標準偏差を計算する関数なのですが、お尻についた「P」と「S」の違いはなんなんでしょうか?
STDEV.PとSTDEV.Sの違い
STDEV.Pは、母集団の標準偏差を計算する場合です。母集団のデータが100個あって、その100個をすべて得ることができ、標準偏差を求めるのであれば、こちらを使います。
STDEV.Sは、母集団から抜き取った標本の標準偏差を計算する場合です。
エクセルのヘルプには、このように書かれています。
■STDEV.S
- 引数を標本と見なし、標本に基づいて母集団の標準偏差の推定値を返します。
- STDEV.S 関数は、引数を母集団の標本であると見なします。指定する数値が母集団全体である場合は、STDEV.P 関数を使用して標準偏差を計算してください。
- 標準偏差は、n-1 法を使って計算されます。
■STDEV.P
- 引数を母集団全体であると見なして、母集団の標準偏差を返します。
- STDEV.P 関数は、引数を母集団全体であると見なします。指定する数値が母集団の標本である場合は、STDEV 関数を使用して標準偏差を計算してください。
- 標本数が非常に多い場合、STDEV.S 関数と STDEV.P 関数の戻り値は、ほぼ同じ値になります。
- 標準偏差は、n 法を使って計算します。
- STDEV.S 関数は次の数式を使って標準偏差を計算します。
標準偏差は、分散の平方根です。計算手順としては、まず、各データの偏差を合計してデータ数で割って分散を計算するわけです。その平方根が標準偏差です。
この計算手順の「データ数で割る」ところに違いがあります。
各データの偏差の合計をデータ数「n」で割るか、「n-1」 で割るかが、STDEV.P と S の違いです。
エクセルのヘルプに掲載されている式を借りてきました。
■STDEV.P・・・nで割る

■STDEV.S・・・n-1 で割る
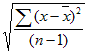
こういった違いがあります。
計算時にn-1 で割る理由
では、なぜ標本の標準偏差は、計算途中でn-1 で割るのか?
標本サイズnが小さいときは、標本の標準偏差は、母集団の標準偏差よりも小さい値になりやすいからです。
細かい話はこちらの記事を参考にしてください。
参考記事 母集団の標準偏差の不偏推定値を計算するときに√n-1で割る理由
また、母集団を標本についてはこちらの記事に書きました。
参考記事 母集団と標本の違い
母集団とは観測対象の全体のことです。私たちがデータを集めて母集団について調べるときには、母集団のデータ数が多ければ多いほど全体を調べることは難しくなります。
たとえば、あるスーパーマーケットに来店したお客さんの意識調査のためアンケートをとりたいと思ったら、お客さん全員が母集団です。
母集団であるお客さんすべてに対してアンケートをとる時間も人手も、ふつうは無いでしょう。となると、できる数のアンケート調査をし、その結果をもとにして母集団つまりお客さん全体がどういった意識を持っているのかを探ろうとします。これが推定です。
あくまでも、私たちが知りたいのは標本ではなくて、母集団についてです。しかし、実際に母集団すべてを調べられないのですから、母集団の標準偏差は不明なのです。
だから、標本の標準偏差から母集団の標準偏差の推定して知ろうとします。
そのときに標本サイズn が小さいと(標本のなかのデータ個数が少ないと)、標本の標準偏差は実際の母集団の標準偏差よりも小さくなりやすいのでズレが出てしまいます。これでは困りますよね。
それを補正するために、n-1 で割るのです。n-1 で割れば、そのぶん少しだけ値が大きくなりますよね。
ところで、
n-1 で割らずに分散を計算して、後から、n/n-1を掛けて平方根をとっても同じ値になり、
n-1 で割らずに標準偏差を計算して、後から、√n/√n-1を掛けても同じ値になります。
つまり、STDEV.Pで出した値に√n/√n-1を掛けるとSTDEV.Sで出した値になります。

STDEV.P とSTDEV.S・・・この「P」と「S」のアルファベットは、なにを表しているのか?
populationとsampleの頭文字でしょう。英語で言うと母集団はpopulationで、標本はsampleです。エクセルのヘルプに書いてあるわけではないですが、まあそうでしょう。
PとS、どちらを使ってもいい
ふつう、なにかデータを集めて標準偏差を計算するときに、母集団すべてのデータを集められることなど少なく、標本を集めて、母集団の特性を推定することがほとんどでしょう。その意味で言えば、STDEV.Sを選ぶのが正しいですよね。
でも、データの数が多ければ、結局どちらをつかっても問題ないです。nが大きくなっていくほど、nとn-1の差はなくなっていきますから、STDEV.Pを使って計算しようが、STDEV.Sをつかって計算しようが、ほとんど変わらない数字になります。ためしに、100個のデータで計算してみましょう。
別の記事で記載したデータです。
とあるメーカーでの製品重量に関する話です。製品の重量を計測すると、次のような120個のデータが得られました。
105、115、107、105、110、105、117、103、117、116、110、119、 120、109、112、118、121、107、109、112、114、115、115、99、 108、114、112、116、105、124、112、117、111、114、112、108、 102、112、105、115、96、105、111、104、107、107、111、121、 118、118、117、117、114、116、119、121、117、110、109、111、 113、116、110、117、115、118、109、109、111、109、105、102、 107、107、110、114、112、109、105、118、108、109、110、119、 105、115、113、113、111、122、111、116、109、110、111、107、 97、104、110、111、110、118、116、104、116、107、118、112、 112、112、116、113、108、115、118、116、114、116、104、112
※単位: g
このデータ120個を使って計算すると、
- STDEV.P → 5.33594…
- STDEV.S → 5.35831…
となります。さらにデータ数を増やして240個の場合で計算すると、データ掲載は割愛しますが、
- STDEV.P → 5.28861…
- STDEV.S → 5.29966…
となりました。0.01~0.02程度の差しかありませんね。さらにデータが増えれば、ほとんど差がなくなっていきます。
厳密には、STDEV.P とSTDEV.S で計算結果の数値は違っているわけですが、ビジネスでつかう分にはわずかな数値の違いは問題ないでしょう。
なにかの数値を見る理由は、その数値を見て意思決定をするためですね。細かく数字ではなく、もっとざっくりとした数字でも意思決定ができれば問題はありません。
0.01とか0.001などわずかな違いなどまったく気にしないですよね。そもそも、そこまで小数点を細かく表示して見たりしません。
ただ、ほんとにわずかなデータしかなくて…というときには、注意が必要で、STDEV.Sをつかったほうがよいという話です。