移動平均の意味や目的、求め方、注意点

移動平均とは、変化しているデータがあるときに、ある範囲のデータの和をその個数で割ったものです。

その平均値をつなぎ合わせたものが、移動平均のグラフです。

移動平均は時系列データで活用するもので、その目的や注意点を理解したうえで使うようにしましょう。

この記事では、移動平均の意味や目的、求め方、注意点について説明しますのでぜひ参考にしてください。

移動平均の意味や目的

移動平均をつかう目的は、時系列データの推移を読み取りやすくするためです。

移動平均の値をつなぎ合わせて折れ線グラフをつくることによって、不規則な変動が除去されてグラフが滑らかになります。

その結果、時系列データがどのように変化しているか、その傾向が読み取りやすくなります。

移動平均のメリットとデメリット

移動平均のメリットは、データの変化の傾向をつかみやすくなることです。細かいデータを見ているだけでは、大きな変化、大きな流れを読みにくいです。

デメリットは、平均化すればするほど個別の情報が読み取れなくなることです。また、ある個所で発生した変化点に気が付きにくくなる場合もあるでしょう。

移動平均で折れ線グラフを滑らかにして、時系列データの傾向を読み取る

あるお弁当屋さんの販売数の話。

新しいお弁当を開発したので、1ヵ月販売をしてみました。するとある程度の売り上げは確保することができたのでした。

日々の売上数はわかるのですが、この販売データを日々の数値のまま眺めていても、今後どうなっていくのか見えてきません。

数値だけを見るのでなく、視覚に訴えるグラフを作成して見てみるのがデータ分析の常套手段です。さっそくグラフをつくってみました。

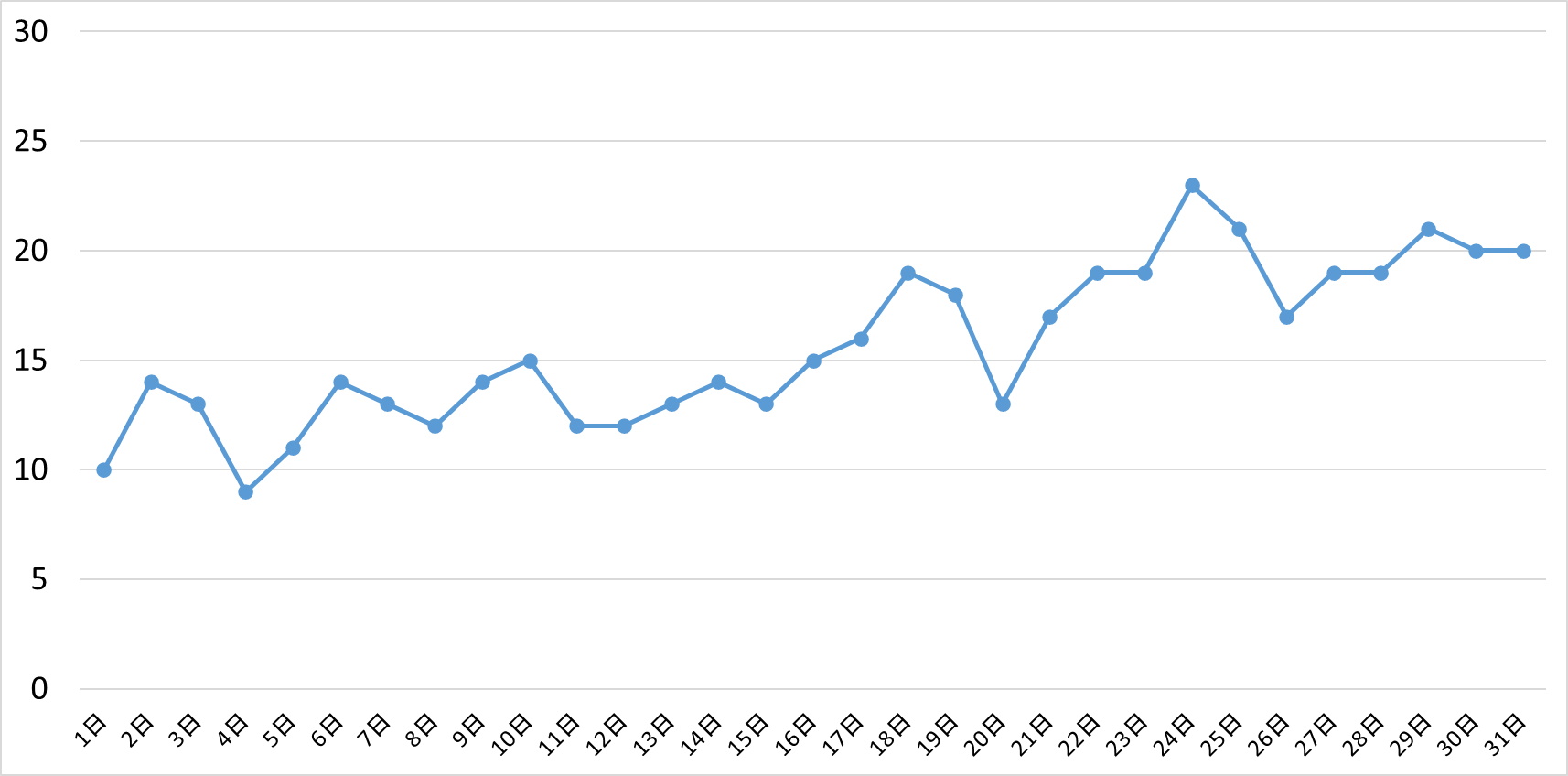
1日あたりの販売数の表や推移グラフ見てみると、なんとなく売上は増えてきているように見えますがどうなのでしょう？

右肩上がりになっているようにも見えますが、どの程度右肩上がりになっているのか、いまいちつかめません。

そこで、移動平均を活用して、どんな具合で売上が推移しているのか見ることにしました。

1日あたりの販売数の推移グラフでは、売上が多い日もあれば少ない日もあり、グラフがジグザグしています。このグラフを滑らかにするため、まず3日間の平均値を計算してグラフをつくります。

移動平均の求め方

3日間の移動平均の求め方としては、

• 1日目、2日目、3日目のデータの平均を、2日目のところに当てはめる
• 2日目、3日目、4日目のデータの平均を、3日目のところに当てはめる
• 3日目、4日目、5日目のデータの平均を、4日目のところに当てはめる

こんな感じで平均値を出してつなげていきます。5日分の売上を再掲しました。こちらで実際に計算してみます。

1日目	2日目	3日目	4日目	5日目
10個	14個	13個	9個	11個

・1日目・2日目・3日目の平均

（10個＋14個＋13個）/ 3 ＝ 12.33

これを2日目のところに当てはめます。

・2日目・3日目・4日目の平均

（14個＋13個＋9個）/ 3 ＝ 12.00

これを3日目のところに当てはめます。

・3日目・4日目・5日目の平均

（13個＋9個＋11個）/ 3 ＝ 11.00

これを3日目のところに当てはめます。

するとこちらの表のようになります。

1日目	2日目	3日目	4日目	5日目
	12.33個	12.00個	11.00個

このような具合で、29日目・30日目・31日目の平均まで計算します。

最初の1日目と最後の31日目に当てはめるデータは、計算しません。一番端のデータで片方の隣にはデータがありませんから、3日分をまとめたデータを計算することができず、値は無しになります。

これをグラフにすれば、3日間の移動平均のグラフができます。

3日間の移動平均

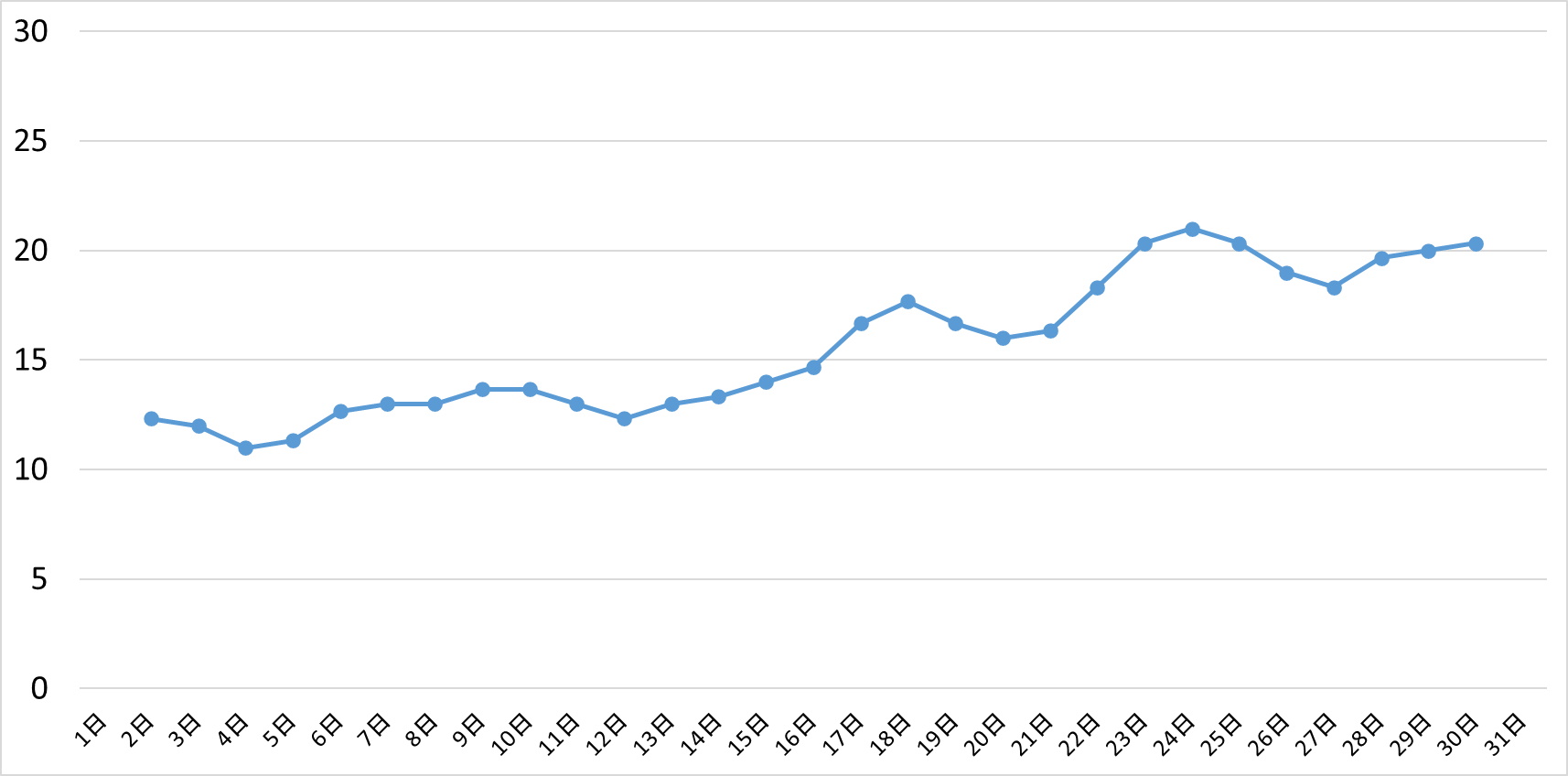
生データのグラフは、毎日の売上が上がったり下がったりして、線がデコボコとしていましたが、3日移動平均の線は滑らな線になっていますね。

移動平均には、生データの不規則な変動をならし、時系列データを平滑化させて傾向をみやすくする役目があります。

グラフが滑らかになることで、傾向が読み取りやすくなるのです。

さらに5日移動平均もつくってみると、線がさらに滑らかになり、売上が伸びてきていることが容易にわかるようになりました。

5日間の移動平均

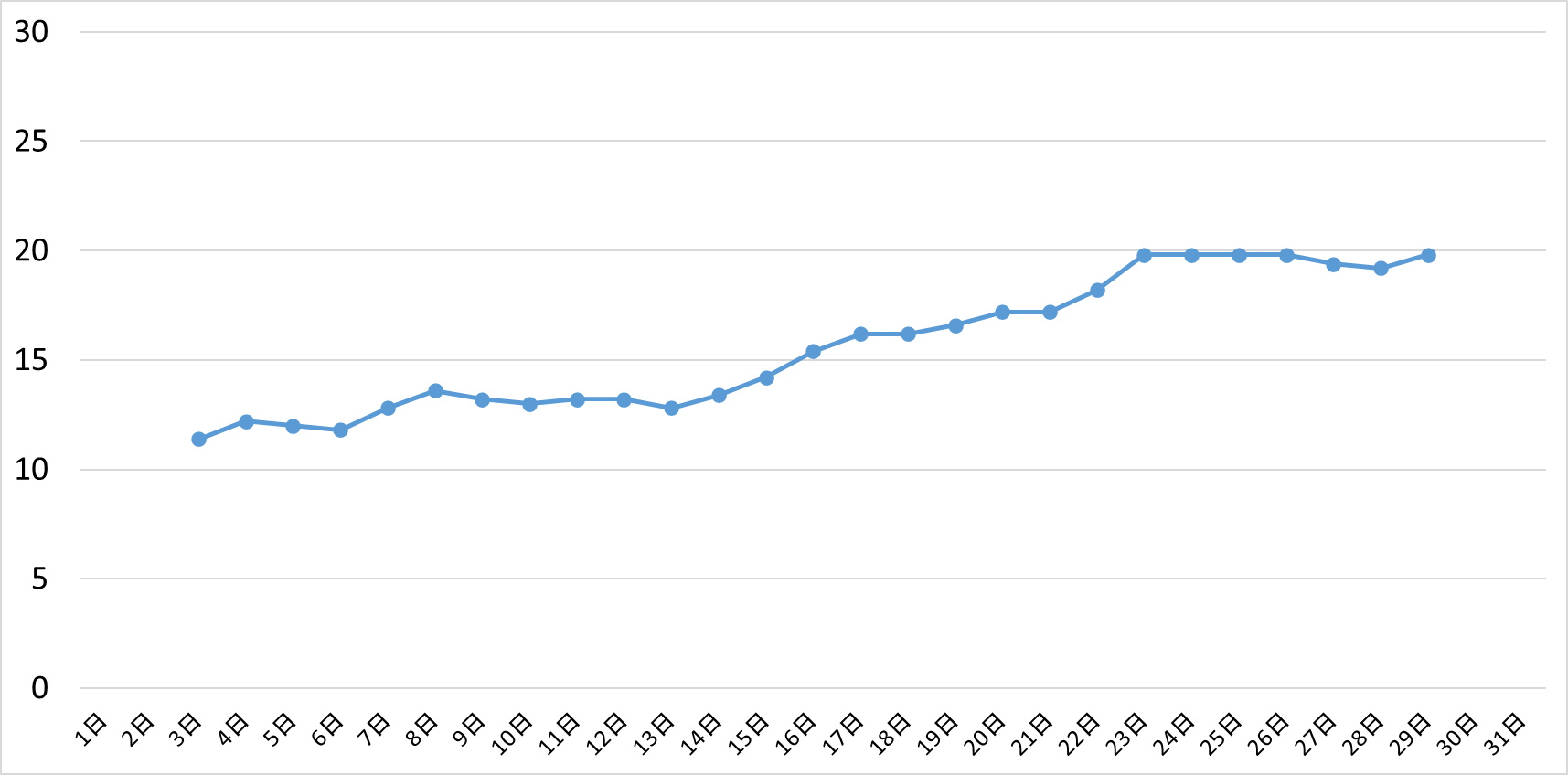
3点の平均をとるのであれば3点移動平均、5点の移動平均をとるのであれば5点移動平均といいます。

このお弁当販売の話では、1日あたりの売上を見ていくので、3日移動平均とか5日移動平均と呼ぶことになります。

さらに移動平均につかう日数を増やしていくと・・・、

7日間の移動平均

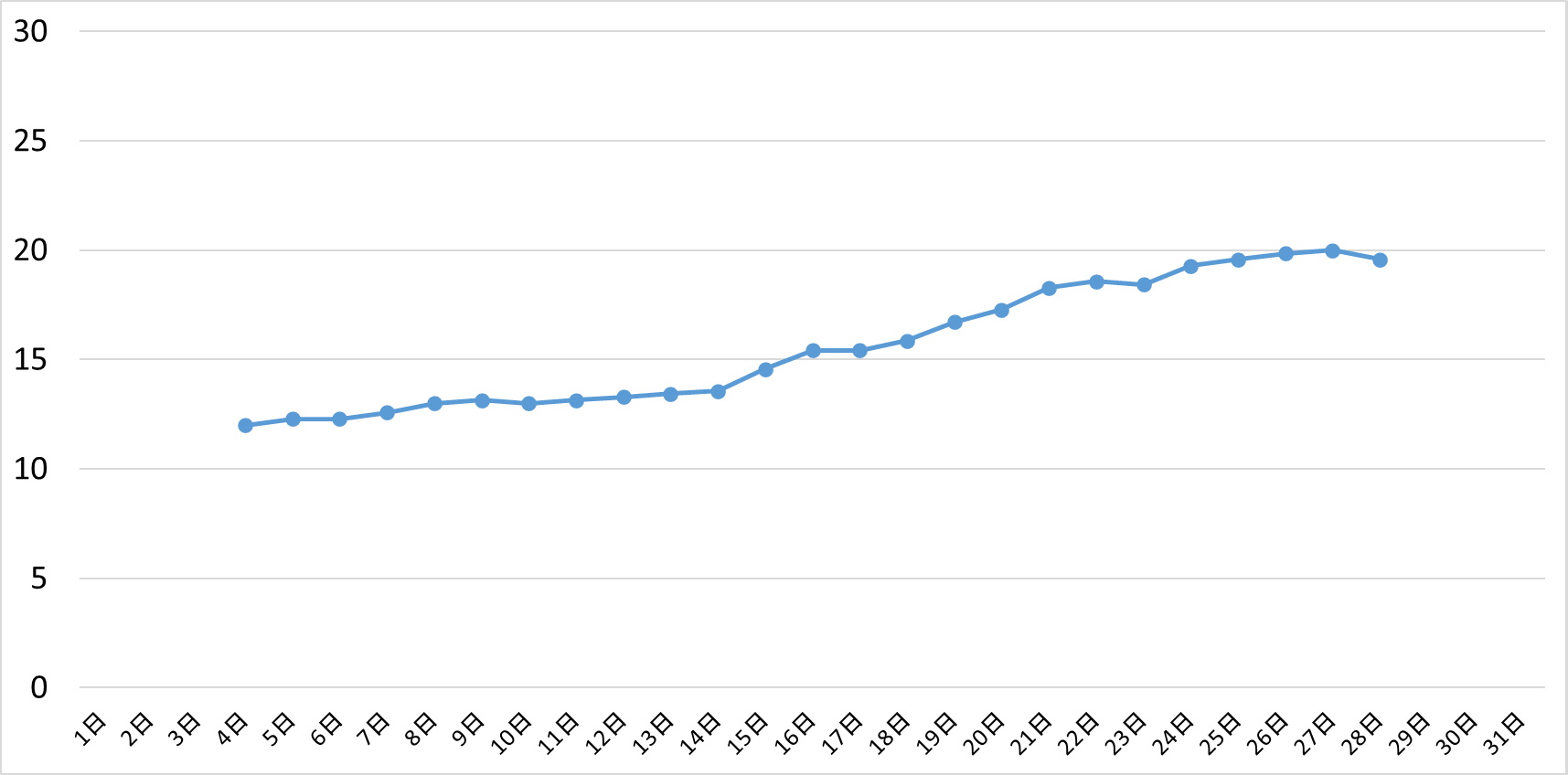
9日移動平均

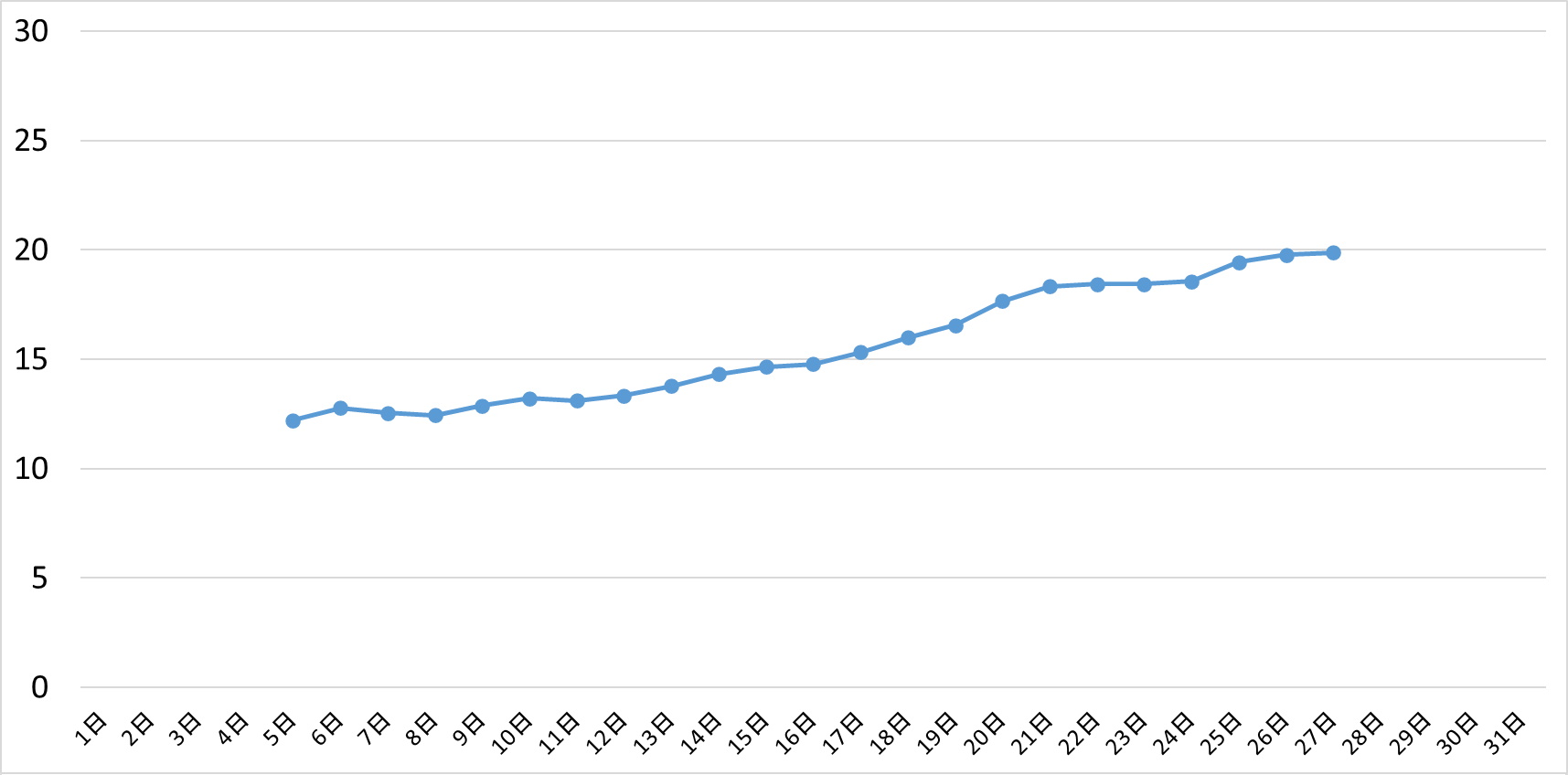
さらに極端にすると、

29日移動平均

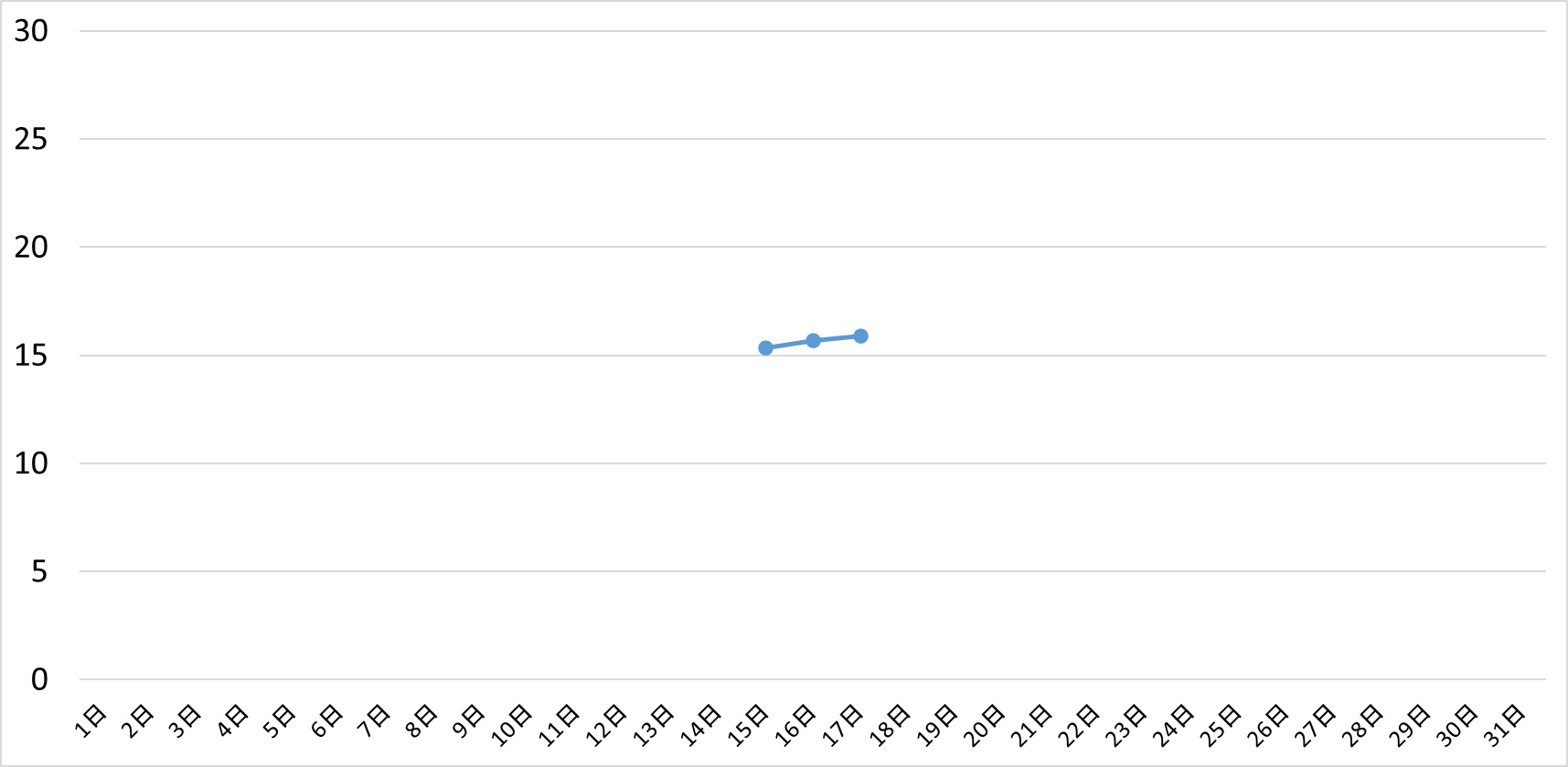
31日移動平均

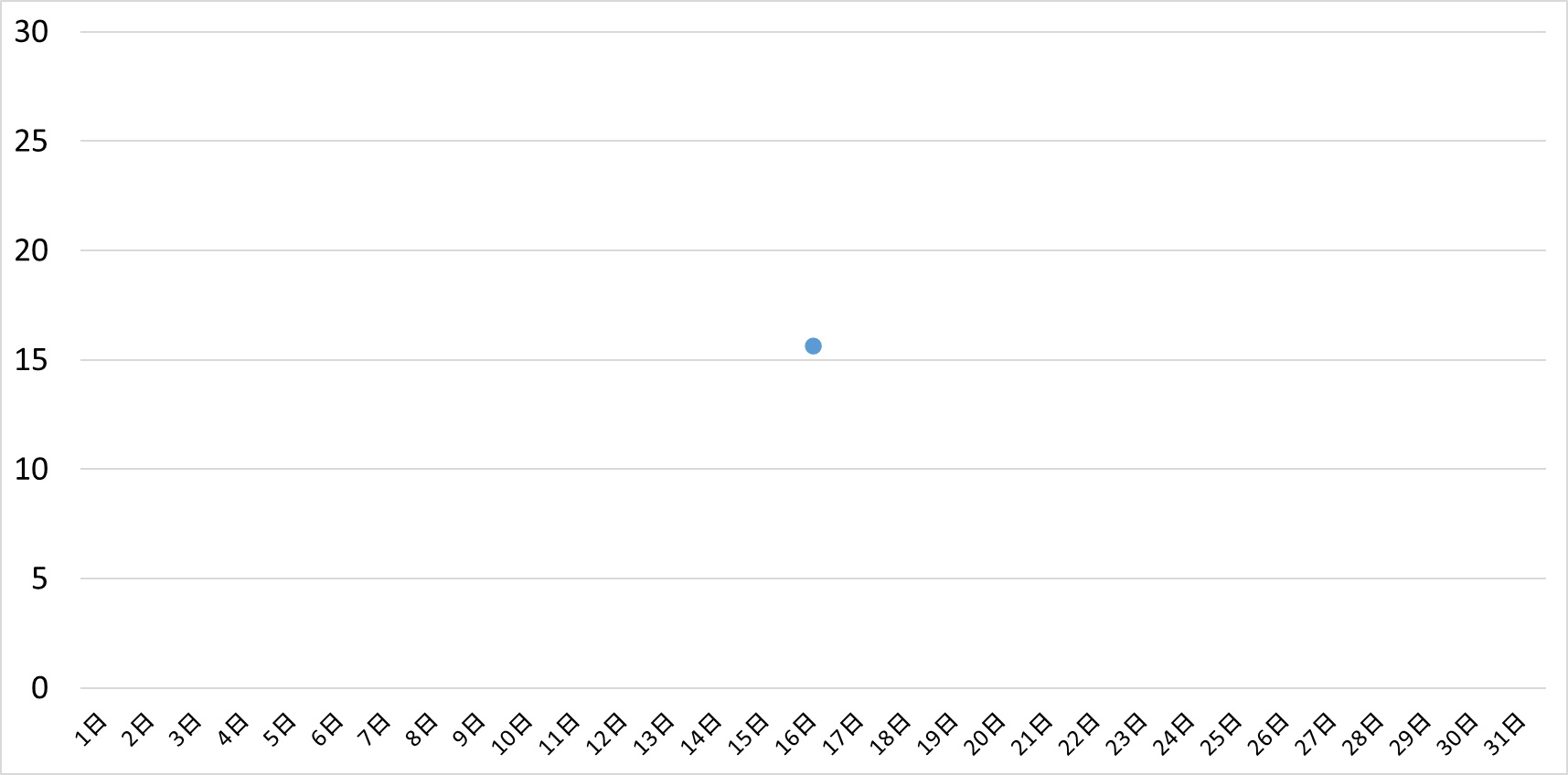
31日移動平均線は、データは16日の上に1点だけになってしまいました。これは、31日間のデータを単純に平均した値と同じになります。

移動平均を活用するときの注意点

平均の計算対象とする期間を長くしすぎないこと

上にのせたグラフのように平均する日数を増やしていくと、どんどんグラフが滑らかになっていくとともに、端の部分が計算できないので線の長さが短くなっていきます。

これは、お弁当がたくさん売れた日、あまり売れなかった日などの日々のデータが平均化され、生データの情報が失われていることを意味します。

もともとのデータ数が多い場合はいいのですが、少ない場合はデータの損失はあまり望ましくありません。

移動平均のメリットは、傾向をつかみやすくなることですが、平均化すればするほど、個別の情報が読み取れなくなるデメリットがあります。

9日間の移動平均を見てみると売上が上昇傾向にあることは一目でわかるのですが、とても滑らかなので、日々の個別データの情報は、ほとんどわからないですよね。

・9日移動平均

31日間の移動平均線は極端な例ですが、もはや線ではなく点ですから、上のグラフの中では最も情報量が少なくなります。

・31日移動平均

移動平均を使うのは、データ推移の傾向を読み解くことが目的です。であれば、5日移動平均線程度の平均化であっても十分に傾向がわかりますね。

・5日移動平均

それ以上の滑らかさを求めてデータの損失を増やす必要はありません。

そもそも、生のデータのグラフの状態でも、傾向をはっきりと読むことができる状態であれば、移動平均を用いる必要も無いといえます。

適切な間隔でデータをとること

時系列データは、時間の変化にともなって変化するデータを記録していくわけですが、その間隔が適切でないとデータが正しく読み取れません。

データをとるのは等間隔がよい場合が多いでしょう。また、細かくとりすぎてもダメですが、間隔が開きすぎてもダメです。

弁当屋の例で考えてみると、最初は毎日データをとっていたのに、1ヵ月後には2週間に1回だけデータをとるようになった。こうなると、2週間の間の変化がわからなくなります。これで移動平均を見たらもっとわからないです。

さらに、2週間に1回データをとる曜日が毎週決まった曜日ではなくて、月曜日であったり、水曜日であったり、日曜日であったりしたらどうでしょう。

曜日によって売り上げが変わっているとしたら、曜日の影響が出てきてしまうので、正しい変化が見られないかもしれないですね。

まとめ

以上、移動平均について説明しました。

移動平均を使うと、不規則な変化が除去されて滑らかな変化がつくりだされ、データの推移が読み取りやすくなります。

注意点を意識しながら、うまく活用したいですね。

最後まで読んでくれて、ありがとうございました！