平均値と分散を持つ2つのものがあったときに、それらを合わせたものの分散は、それぞれの分散を足し合わせた値になります。このことを「分散の加法性」といいます。
2つの確率変数XとYがあって、XとYが独立であるときには、XとYを合わせたものの分散は、X+Yとなるのです。また、XからYを引いたものの分散も同じくX+Yとなります。
$$V(X±Y) = V(X) + V(Y)$$
が成り立ちます。
※ちなみに期待値については、
$$E(X+Y) = E(X) + E(Y)$$
が成り立ちます。
部品を合わせてつくる製品の寸法のばらつき
たとえば、部品A、部品Bの2つの部品を組み合わせて製品をつくる場合、完成品の長さの分散は、「部品Aの分散」と「部品Bの分散」を足し合わせた数値になります。どの部品Aが選ばれるか、どの部品Bが選ばれるかは互いに影響を与えず、独立していなければなりません。
- 部品Aの分散は、σ2A
- 部品B分散は、σ2B
であるとしたら、完成品の分散 σ2 の計算式は、
| σ2 = σ2A + σ2B |
となります。
次の2つの部品をくっつけて作る製作物があったとします。完成品の長さとそのばらつきは、どのようになるのか見てみましょう。となります。
- 部品A……長さ平均20mm、分散1mm
- 部品B……長さ平均30mm、分散1mm
このような部品があります。
部品AとBを組み合わせたものの長さの平均は、
| 完成品の平均 = 部品Aの平均 + 部品Bの平均 |
20mm + 30mm = 50mmの式で計算できます。
となります。
分散の計算式は、
| 完成品の分散 σ2 = 部品Aの分散 + 部品Bの分散 |
ですから、
完成品の分散σ2 = 1 + 1 = 2
完成品の分散は2mmで、正の平方根をとる標準偏差は√2です。
標準偏差σ= 1.4mm
となります。
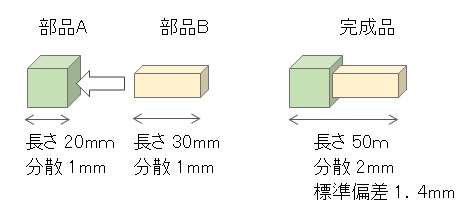
完成品は、平均の長さが50mmで、標準偏差は1.4mmになります。
ただし、分散の加法性が成り立つのは、「部品Aの分散」が正規分布をしていて、「部品Bの分散」も同じく正規分布をしているときです。正規分布しているなかから、ランダムに部品が選ばれたときです。
複数の製品をまとめたときの重量のばらつき
複数の製品をまとめたときの重量について考えてみましょう。これも分散の加法性がつかえるのですね。
|
製品複数個の重量の分散σ2 = 1個目のσ2 + 2個目のσ2 + n個目のσ2 =σ2 × 個数n |
となります。
1個の重さが平均50gで、分散が4g、標準偏差が2gの製品があったとしましょう。
この製品を6個をケースに入れてまとめると重量の平均と分散はどうなるのか。当然のながら、重量の平均は50gが6個なので、平均300gになります。(ケースの重さは除いて考えています。)
300gである製品を6個全体のばらつき(分散)はどうなるかというと、製品それぞれの分散を足し合わせればいいのですから、
4g+4g+4g+4g+4g+4g = 24g
6個をまとめたケースの分散は、24gになるのです。標準偏差は、√24 = 4.9gになります。
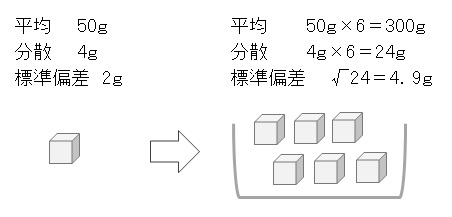
このように、分散の加法性を活用すれば、あるものとあるものを合わせたときの分散がどうなるのか、計算することができます。
差の分散も加法性が成り立つ
また、あるものからあるものを引いたときにも、分散の加法性が成り立ちます。
たとえば、ここにあるリンゴの山があり、
- リンゴの重さ平均300g、分散10g
の正規分布にしたがっているとします。
リンゴの山からリンゴを2つ取りだしたときに、その2つのリンゴの重量差の分布はどうなるのか?を考えます。ひとつめに取りだしたリンゴの重量から、ふたつ目に取りだしたリンゴの重量を引くことにしましょう。これを繰り返します。
あるときは、たまたまひとつめのリンゴが重いかもしれませんし、軽いかもしれません。でも、2つ取りだしてリンゴ2個の重量の差を計測することを繰り返していれば、2つのリンゴの重量差は、平均的には0となるでしょう。
で、分散はどうなるかというと、ここでも分散の加法性が成り立ちます。
2つのリンゴの重量差は、平均0g、分散20g
となるのです。
また次のようなことでも考えることができます。
部品Aに穴をあけるとします。部品Aの長さは正規分布をしていて、穴の深さも作業に多少の誤差が発生して、穴の深さは正規分布しているものとしましょう。
- 部品A……長さ平均20mm、分散1mm
- 穴……深さ平均10mm、分散1mm
穴の底から部品Aの反対面までの長さはどうなるのか?穴を掘って残った部分の長さですね。
残り部分の平均 = 部品Aの平均 - 穴の平均
で計算できます。
20mm - 10mm = 10mm
となります。
分散の計算式は、
残りの部分の分散σ2 = 部品Aの分散 + 穴の分散
ですから、
分散 σ2 = 1 + 1 = 2
正の平方根をとる標準偏差は√2 = 1.4mm となります。
穴を掘って残った部分の長さは、平均10mm、分散2mm の正規分布にしたがいます。平均の差であっても、分散は広がっていきます。