ヒストグラムの階級数を決めるときには、スタージェスの公式が参考になります。
スタージェスの公式とは、ヒストグラムを作成するときに、階級の幅の目安を決めるための数式です。
度数分布表およびヒストグラムを作るときには、階級数、階級幅をどうするかが問題です。
階級数が少なすぎてグラフがドテッとすると、分布が読みとれないのでダメですし、
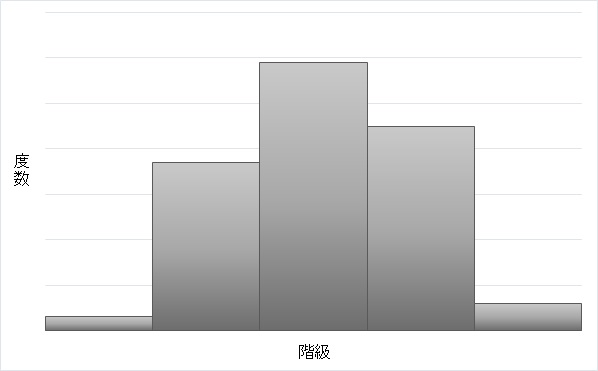
逆に、階級数が多すぎて歯抜け型になってもいけません。階級の幅を狭くしすぎて、データが不足しています。
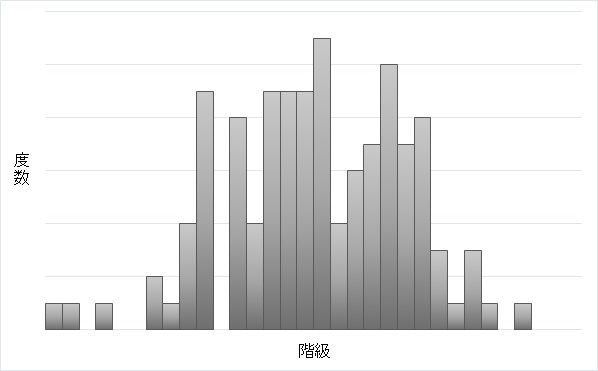
ヒストグラムの目的とは、得られたデータに関しての理解を手助けをすることであり、現象の背景にどういったことがあるか見ていきたいわけで、それにかなうグラフにしないといけませんよね。
設定に決まったルールはないですが、参考として
スタージェスの公式
があります。スタージェスの公式で求めた階級幅がベストというわけではなく、あくまで目安です。
データ数をnとして、階級数をkとすると次の式となります。
| k=1+log2n |
64個のデータの場合、
k=1+log264
k=1+6
k=7
100個のデータの場合、
k=1+log2150
k=1+7.228
k≒8
となります。
データ数nと、スタージェスの公式で計算した階級数は下記のようになります。
| データ数n | 階級数 |
|---|---|
| 10 | 4.3 |
| 20 | 5.3 |
| 30 | 5.9 |
| 40 | 6.3 |
| 50 | 6.6 |
| 100 | 7.6 |
| 200 | 8.6 |
| 300 | 9.2 |
| 400 | 9.6 |
| 500 | 9.9 |
| 1000 | 10.9 |
対数の計算は、手計算できるものは手計算で、難しくなってきたらエクセルのLOG関数が使えます。あるいは、関数電卓ですね。
※logについては、log(ログ)を使った対数の意味と表し方に簡単に書いています。
まあ、スタージェスの公式をつかって計算しなくても、いろいろ試してみて決めるもよいです。さほど時間もかかりませんから。
昔は手書きでグラフをつくっていたのでしょうから、まず正しい階級数をしっかり決めてからグラフをつくりださないと、後でやり直しになってしまい大変だったでしょう。
現代は、コンピューターをつかってヒストグラムをつくれます。階級数を間違えたな、と思っても、すぐに作り直すことができますから、そうやって決めるのもよいでしょう。