母平均の推定とは、標本の平均から、母集団の平均を推定することですが、一つ問題があります。
「標本から計算した分散や標準偏差は、母集団の分散や標準偏差と比べて小さいほうへ偏る」
こういう性質があります。
母集団の平均値の区間推定するときに、母集団の標準偏差\(\sigma\)がわかっていてつかえればいいのですが、わからないことが多いです。
となると、標本データから計算した標準偏差をつかって、母集団の平均値を推定することになります。
が、標本データから計算した標準偏差は、母集団の標準偏差よりも、小さい方に偏ってしまう性質があります。
そのために標本データから計算した標準偏差または分散は補正をかける必要があります。その方法が、分散を計算するときに\(n-1\)で割ることです。
この記事では、その\(n-1\)を用いる理由について解説していきます。
母平均の点推定・区間推定についてまだわからない方は、下記の記事を先に読んでいただけるとよいと思います。
参考記事 点推定と区間推定について説明した記事
標本の標準偏差を補正するのがn-1
標本から得られた標準偏差は、母集団の標準偏差と比べて、小さいほうへ偏ってしまう。
この問題を解決するために、そのため標本の標準偏差$s$は、そのまま母集団の標準偏差として考えるのでなくて、補正をかける必要があります。
補正をかけたものを、母集団の標準偏差の推定値として考えるのです。
その補正の方法が、
- 標本の分散に\(\frac{n}{n-1}\)をかける、あるいは、
- 標本の標準偏差に\(\sqrt{\frac{n}{n-1}}\)をかける
です。
次のような標本データがあります。
5つの値の平均値は、100g。これを母集団の平均の推定値としますが、実際の母集団平均は100gよりも大きいかもしれないですし、小さいかもしれません。
それは神のみぞ知ることです。
私たちがわかるのは、この5つのデータとそこから得られる平均値100gという数値です。
そして、母集団の標準偏差を推定するにしても、標本のデータから得られたこの100gの数値を使って、標準偏差を計算することになります。
標本標準偏差が小さい方に偏る理由
標本データから計算された標準偏差は、母集団の標準偏差と比べて、小さいほうへ偏ってしまいがちなのです。これは、なぜでしょうか。
標準偏差の計算の流れは、各データの偏差をだして、二乗して、足し合わせて、データ数で割り、平方根をとる、です。
偏差をもとにして、標準偏差が計算されていますよね。
データ数がn個のときの標準偏差の計算式
$$s=\sqrt{\frac{1}{n}\sum_{i=1}^n (x_i -\bar{x})^2}$$
ですので、偏差を二乗して足し合わせた数値(偏差平方和)が大きいほど、標本の標準偏差の値は大きくなり、偏差平方和が小さいほど標本の標準偏差の値は小さくなります。
標本データの平均値をつかって標準偏差を計算すると、自動的に、偏差平方和がもっとも小さくなるようになっています。つまり、偏差平方和をnで割って平方根をとった数値である標準偏差も、同様にもっとも小さくなってしまうのです。
その理由は、そうなるように、標本の各データが平均値を決めてしまっているからです。
標本のデータで平均値を計算すれば、当然、平均値はそれらデータの真ん中に位置します。そうなったときが、偏差平方和がもっとも小さくなり、仮に標本の平均値からズレた値を平均値としてしまって計算すると、偏差平方和は大きくなります。
さきほどの5つの製品の重量データを用いて、試しに計算してみましょう。
この5つのデータの平均値は100gです。まず100gの値をつかって、まず分散・標準偏差を計算していきます。
次に、99gの場合、101gを平均値として計算してみます。
平均値を100として標準偏差を計算
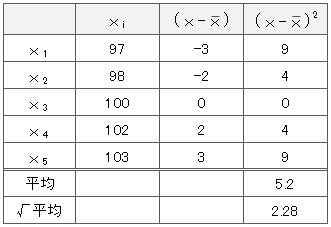
分散は、
$$=5.2$$
標準偏差は、\(\sqrt{5.2}=2.28\)
となります。
標本の平均が100gだからといって、母集団の平均値は、100であるとは限りません。仮に99であったして、分散・標準偏差を計算してみます。
仮に平均値を99として標準偏差を計算
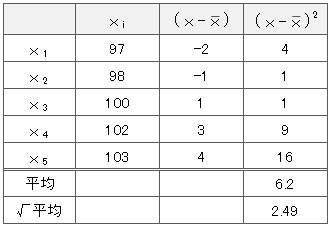
分散は、\(6.2\)
標準偏差は、\(\sqrt{6.2}=2.49\)
となります。
となり、標本の平均値である100を使って計算するよりも標準偏差が大きくなりました。
これは、平均値を101として計算しても同じ値になります。
仮に平均値を101として標準偏差を計算
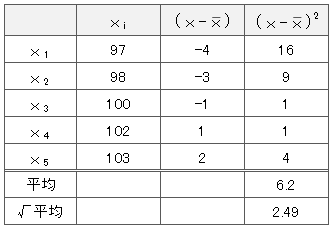
同じく、
分散は、\(6.2\)
標準偏差は、\(\sqrt{6.2}=2.49\)
となります。
このように、標本の平均値で計算する標準偏差は、一番小さくなるようになっているのです。
よって、標本標準偏差\(s\)は、母標準偏差\(\sigma\)よりも小さいほうへ偏りがちになるので、そのままでは母標準偏差\(\sigma\)の推定値としては使えません。推定値として使うためには、補正をかける必要があります。
※母標準偏差とは、母集団の標準偏差のことです。
標本の標準偏差にn-1で補正をかける
その補正の方法は、下記の計算でできます。
母集団の標準偏差\(\sigma\)の推定値の計算方法は、
標準偏差を計算してから、\(\sqrt{\frac{n}{n-1}}\)を掛ける。
$$\hat{\sigma}=s×\sqrt{\frac{n}{n-1}}$$
または、
標準偏差を計算する過程で、偏差平方和\(\sum_{i=1}^n (x_1-\bar{x})^2\)を\(n\)で割るのでなくて、\(n-1\)で割るでもいいです。
$$\hat{\sigma}=\sqrt{\frac{1}{n-1}\sum_{i=1}^n (x_1-\bar{x})^2}$$
計算するとどちらも同じ数値になります。
標本の平均値の100をつかって標準偏差を計算した表を再掲します。

標本の標準偏差は、2.28です。
母標準偏差の推定値は、標本サイズ\(n\)が5個ですから、標本標準偏差に\(\sqrt{\frac{5}{5-1}}\)を掛けた数値が推定値になります。
$$2.28×\sqrt{\frac{5}{5-1}}=2.55$$
2.28 →2.55 と変わりました。
標本の標準偏差は小さい方へ偏ってしまいがち、とお伝えしました。補正によって少し大きな値になりましたね。これが、母集団の標準偏差の推定値になります。
もうひとつの計算方法である、標準偏差の計算途中で、偏差平方和をデータ数\(n\)で割るときに、「\(n\)」ではなく「\(n-1\)」で割って計算する方法でも同じ値が得られます。
$$分散=\frac{偏差平方和}{n-1}$$
$$=\frac{26}{5-1}=6.5$$
標準偏差は、
$$\sqrt{6.5}=2.55$$
ただし\(n\)が大きくなれば、「\(n-1\)」で割ったりすることなく、標本の標準偏差\(s\)をそのまま、母集団の標準偏差\(\sigma\)の推定値として使用しても大丈夫になります。
なぜなら、標本の数が増えるほど、数値の大きさの割には「\(n\)」と「\(n-1\)」の差が無くなるからです。
\(n\)=1,000,000であったら、偏差平方和はかなり大きな値になっています。それを\(n\)の1,000,000 で割っても\(n-1\)の999,999 で割っても、その結果にはほとんど差がなくなっています。
母集団の分散の不偏推定値を計算
$$\hat{\sigma}=s×\sqrt{\frac{n}{n-1}}$$
$$\hat{\sigma}=\sqrt{\frac{1}{n-1}\sum_{i=1}^n (x_1-\bar{x})^2}$$
の二つの式で、計算をしてみましょう。
母集団の分散の不偏推定値の平方根をとると、標準偏差となります。
標本から計算した平均値100を使って分散の推定値を計算すると、
$$分散=\frac{偏差平方和}{n}\\=\frac{26}{5}=5.2$$
です。母集団の分散の不偏推定値は、\(\frac{n}{n-1}\)をかけますから、
$$5.2\times\frac{5}{5-1}=6.5$$
6.5の平方根をとると標準偏差の推定値になります。
$$\sqrt{6.5}=2.55$$
二つ目の計算方法。データ個数nで割ってふつうに計算した標本の標準偏差に、\(\sqrt{\frac{n}{n-1}}\)をかけても同じ値になります。
$$2.28\times\sqrt{\frac{5}{5-1}}=2.55$$
\(2.55\)で同じ値になりました。