分散・標準偏差を区間推定するには

分散・標準偏差の区間推定のやり方について書きました。

あるメーカーで製品をつくった時に、どのくらいの重量なのだろうと、秤にのせてはかってみたところ次のようなデータが得られたとします。

97ｇ、98ｇ、100ｇ、102ｇ、103g

製品は毎日毎日つくられており、これからもつくられていくものですので、無限母集団と考えます。そこから取り出した標本がこの5つです。

母集団の分散は、次の式で推定することができましす。$\hat{\sigma}$のように「^」マークがつくと、推定値であることをあらわしています。

☆母集団の分散の不偏推定値

$$\hat{\sigma}^2=s^2×\frac{1}{n-1}$$

これで分散または標準偏差の1点の推定はできても、区間推定をすることができません。

区間推定をするためには、$\chi^2$分布と呼ばれる分布を活用します。

偏差平方和を$\sigma^2$で割った値が$\chi^2$値です。この$\chi^2$値がどういった分布をするのかを見ることで区間を推定することができます。

$$\chi^2=\frac{(x_1-\bar{x})^2+(x_2-\bar{x})^2+…+(x_n-\bar{x})^2}{\sigma^2}$$

または、

$$\chi^2=(\frac{x_1-\bar{x}}{\sigma^2})^2+(\frac{x_2-\bar{x}}{\sigma^2})^2+…+(\frac{x_n-\bar{x}}{\sigma^2})^2$$

偏差平方和を大文字の「$S$」で表すと、

$$\chi^2=\frac{S}{\sigma^2}$$

という式にできます。

偏差平方和は、各データの偏差を二乗した値を足し合わせたものですから、データの数が増えるほど、偏差平方和は大きくなります。同時にχ²値も大きくなってしまいます。

区間推定の範囲が変ってしまうので、データ個数によって、それぞれ分布が存在しています。

標準偏差の区間推定の計算方法

上記した5つのデータの偏差平方和は、

$$(97-100)^2＋(98－100)^2+(100-100)^2+(102-100)^2+(103-100)^2=25$$

偏差平方和は26です。

$$\chi^2=\frac{S}{\sigma^2}$$

$$\chi^2=\frac{26}{\sigma^2}$$

ここで、自由度が登場します。自由度とは、データ数ｎ-1 の値のことです。この自由度の値がいくつなのかによって、区間推定をするためにつかう$\chi^2$分布の形が変わります。

自由度は、

自由度$＝ n-1$

$＝ 5-1$

$＝ 4$

となります。

自由度＝4の$\chi^2$分布グラフを見てみましょう。

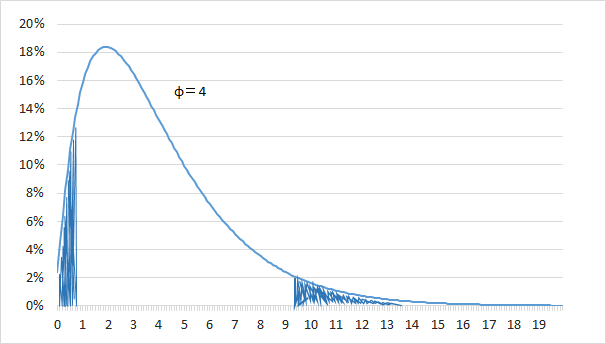
塗りつぶした箇所が下側5％と上側5％の区間です。この間が90％の信頼区間になります。

下側5％と上側5％の$\chi^2$値はそれぞれ、

下側　0.711
上側　9.49

です。

この値は、$\chi^2$分布表で確認することができます。 $\chi^2$分布表とは、各自由度ごとに、「○○％の確率で$\chi^2$（Ｓ/σ²）の値が○○になる」といった数値が、記載されている表です。

自由度＝1 の場合で、下側5％の確率となる$\chi^2$値は・・・

自由度＝2 の場合で、下側5％の確率となる$\chi^2$値は・・・

といった具合です。

$\chi^2$値は90％の確率で0.711～9.49の間におさまることになりますので、

$$0.711<\chi^2<9.49$$

と式をつくることができ、$\chi^2=\frac{Ｓ}{\sigma^2}$ですから、

$$0.711<\frac{S}{\sigma^2}<9.49$$

になります。上で計算した偏差平方和を代入すると、

$$0.711<\frac{26}{\sigma^2}<9.49$$

となります。これを計算していきましょう

分子と分母をひっくり返すと、不等号の向きが逆となります。

$$\frac{1}{0.711}>\frac{\sigma^2}{26}>\frac{1}{9.49}$$

26を掛け算すると、こうなります。

$$\frac{26}{0.711}>\sigma^2>\frac{26}{9.49}$$

$$36.568>\sigma^2>2.739$$

このままでは分散ですから、標準偏差にするため平方根をとると、ほぼ

$$6.047>\sigma>1.655$$

となりました。母集団の標準偏差$\sigma$の90％信頼区間は、1.655～6.047となりました。