統計学でパン屋の不正を見破ったポアンカレの話

19世紀から20世紀にかけてのフランスに、ポアンカレという数学者がいて、統計学を使ってパン屋の不正を見抜いた逸話があります。

パンの重量は1000ｇを平均として正規分布するはず…

あるパン屋では1000gのパンが売られていました。1000gのパンをつくるには、当然1000gを目指してつくりますが、その重量からは少し重くなったり、少し軽くなったりしてしまうものです。要するにある程度の誤差が生まれます。ただ、その誤差は大きいものほど発生しにくいのが普通です。

1020ｇになったり、980ｇになったりすることはよくあるでしょう。1050ｇになったり、950ｇになることもあるかもしれません。しかし、1100ｇになったり、900ｇになったりすることはまずないといえますよね。これは、誤差と呼べるものではなくて、なんらかの大きな間違いがあったのだろうと考えることができます。

パンに限らず、基本的にある重量をねらってつくった製品は、ねらいの重量ジャストの製品だけがつくられるわけではなく、誤差が生まれます。その誤差は、正規分布すると考えられます。

つまりパンの重量は重いもの軽いものが色々できて、正規分布をするということになります。

平均値を算出し、データの分布をグラフにする

ポアンカレは毎日とあるパン屋で1000gのパンを買っていました。ポアンカレはこのパンの重さを調べて、記録をしていきました。

ところで、ポアンカレはこんな人です。

フリー百科事典『ウィキペディア（Wikipedia）』から転載

ポアンカレは、そのデータの分布をグラフにして見てみました。

正規分布（に近似した分布）ではあったのですが、頂点が950gとなっていることがわかりました。正規分布の頂点は、平均値と同じ値になりますから、パンの平均値は950gであったわけです。

パンの重量は当然1000g基準でつくられているわけなのだから、1000gが平均になるのが普通です。1000ｇを平均にして軽くなったり重くなったりして、誤差があるはずなのです。これは多少であればしょうがないことです。軽い980gのパンがあったとしても、今度は1020gのパンを手にすることもあるかもしれませんから、まあいいかみたいな感じです。

しかし、平均値は1000gでないのは、おかしいのです。

ポアンカレがはかったパンの重さは、平均値が1000gではなくて、950gとなっていたのです。ポアンカレは、パン屋の主人が950gのパンになることをねらってつくっていたことを見抜きました。

パン2～3個の重さが950g であっただけでは、パン屋の主人は、「それはたまたまでしょう」ということができましたが、毎日パンの重さを測って、1年間の蓄積したデータの前には、返す言葉がなかったでしょう。

母平均の検定をすれば完璧です。

パン屋が毎日毎日つくるパンが母集団であり、ポアンカレが買って手に入れたパンは標本として考えられるので、母平均が1000ｇであると仮定した場合に、このように1000ｇよりも軽いパンばかりになるのは偶然に起きたことではないと判断できるかどうかです。

仮説は正しくないと棄却するのであれば、パンを軽くするなんらかの原因が、パン屋に存在していたと考えることになります。

まあ、なんらかの原因ですから、「計量器が壊れていて50g分ずれていたようだ」ともウソを言えるかもしれませんが、さすがに1年間も壊れっぱなしなのもおかしいですね。

グラフの形で不正を見抜く

ポアンカレは、データの分布と平均値を見ることによって、ウソを見破ったわけですが、ここで話は終わりではありません。

パン屋の主人に注意はしたものの、ポアンカレは、その後もパンの重さを調べ続けました。そのデータを用いて重量分布をグラフに表すと、頂点は同じように950gとなっていたのですが、分布の形が変わり、正規分布ではなくなっていました。分布の軽い側（左側）のデータが削られたようになり、そのぶん平均値は950gから少し重くなっていました。

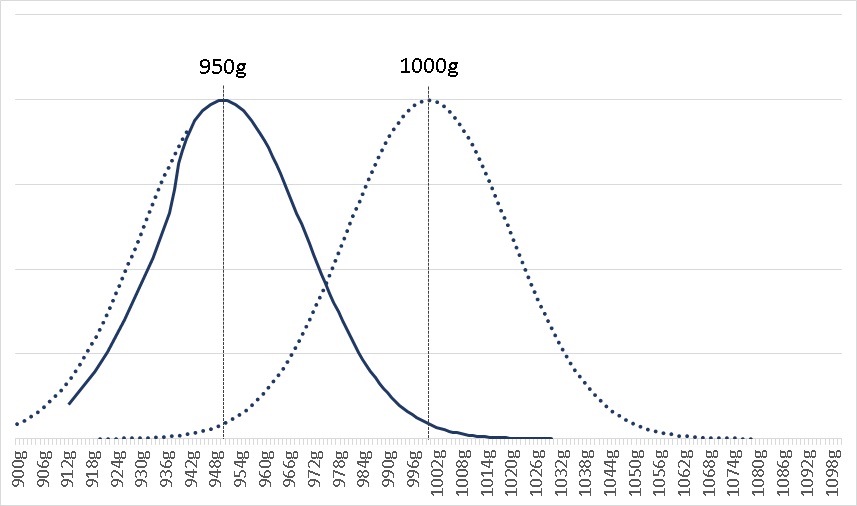
ポアンカレは、このグラフを見て、パン屋になにが起こっているのか、すぐに気が付きました。

パン屋の主人はごまかすことをやめずに、そのまま続けていたのです。そしてポアンカレが来たときにだけ、重そうなパンを選んで渡していた…。ポアンカレはグラフの形からこの不正を見抜きました。

2度のごまかしを見抜かれたパン屋の主人は驚いたことでしょう。

ここから学べることは、本来ならグラフの形が正規分布になるはずなのに、そうはならず、正規分布から形が崩れている場合は、なんらかの異常が起きているかもしれない、ということです。

ヒストグラムの形から背景を読むの記事に書いたように、主なグラフの形として、このようなものがあります。

そのグラグの形ができあがった理由、背景があるはずなのです。

たとえば、層別（QC7つ道具）の意味の記事に書いていますが、分布グラフに2つの山が存在していると、それは性質のことなるデータが混在している可能性が高いと考えられますね。

印象操作するグラフの見せ方の記事では、統計グラフをどのように表すかによって、それを見た人の印象が変わることを書きました。統計学を用いる側も実はウソをつくことができてしまいます。

統計学は、つかうことによってウソをつくこともできるし、ウソを見破ることもできる道具なのです。