ばらつきの原因と思われる要因ごとに集計をして、それぞれのデータの平均値やバラつき、変化などを比較することを「層別」といいます。
母集団をいくつかの層に分けて分析してみることで、結果に影響を与えている要因やデータのバラつきの要因の特定につながります。
層別の方法
層別の切り口を考えるには、データに関する知識や経験をもとになります。
結果に大きく影響を与えていると考えられる要因があったら、その要因を有しているか有していないかで、データを2つに分け、それぞれの平均値など特性値を比較します。
大きな違いがあるのであれば、着目した要因が原因に大きな影響を与えている可能性が考えられます。
それでは、メーカーの製造現場での例をあげてみます。
作業者による製品のばらつき
メーカーの製造現場にて、2人の作業者が製品をつくっているところを考えてみましょう。
この製品の仕上がりは、良いものと悪いものが両方あり、ばらつきが見られていたとします。
その2人の上司は、2人がつくった製品を一緒にまとめてから仕上がりを確認していましたが、作業者の技術レベルに違いあってその影響があるのでは?と考えて、それぞれ1人ずつの製品を分けて、仕上がりを見てみました。
すると、良い仕上がりの製品はひとりの作業者が、悪い仕上がりの製品はもうひとりの作業者がつくっていたものだとわかりました。
ちょっと簡単な例でしたが、要因ごとに分けてデータの平均値やバラつきなどに違いが見られば、それが問題の結果を生み出している原因であるとわかります。原因がわかれば対応策を考えることができます。
母集団が異なる平均値とバラつきをもった複数の異なる集団で構成され、母集団全体のバラつきも大きくなっている状態のとき、これを切り分けることが層別なのです。
もうひとつ例をあげてみます。
同じ機械を2台つかって製品をつくったら
とあるメーカーでのことです。製品重量にばらつきが見られていました。
機械でつくられた製品を計測すると、下のグラフのように重量にバラつきが出てました。
平均値は問題ないのですが、バラつきが大きいために分布の端の軽い製品、重い製品は基準外でロス品になってしまいます。担当者はこのばらつきをもっと小さくしたと考えていました。
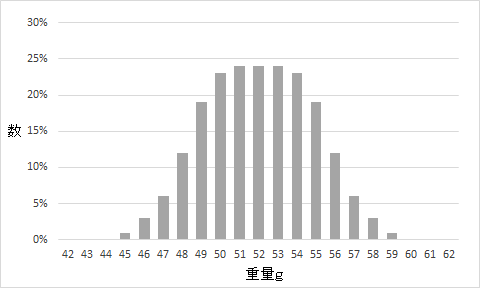
機械は2台使っていて、それぞれの機械でつくられた製品をまとめてから計測をしていました。
ここで層別をつかいます。
いろいろと要因を考えると、機械によって製品重量に違いが出ている可能性もありました。2台の機械でつくった製品を一緒に合わせてしまうのではなく、製品を2台の機械ごとに分けて重量を測ってみました。
すると次のグラフように、平均50gの分布と平均54gの2つの分布が見られたのです。
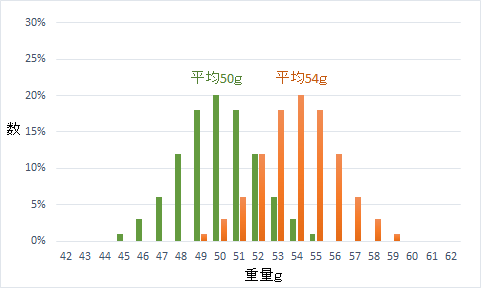
それぞれの機械の設定がずれて、平均50gの分布と平均54gの分布がつくられてしまっており、それが合わさって、平均52gでバラつきの大きい分布になってしまっていたことがわかりました。
それぞれの機械の調整を行い、それぞれの機械で平均52gの製品をつくれるように設定すると、最初の分布よりもばらつきの小さい分布となりました。
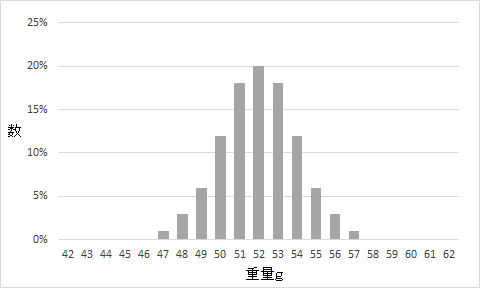
ばらつきの原因と思われる要因が機械ではないかと疑って、機械ごとに分けて製品の分布を比較してみたら、2つの異なる分布ができていたということです。
このように、異なる性質をもった2群が合わさってしまうことで、それぞれの郡の性質が隠れてしまうことがあります。
まとめ
「ばらつきの原因と思われる要因ごとに集計をして、それぞれのデータの平均値、ばらつき、変化などを比較すること」が層別です。
平均が異なった分布が合わさってしまうと、一つの大きな分布のように見えてしまいますが、層別をすることでそれを見抜くことができます。