エクセル関数BINOM.INVの使い方

BINOM.INV 関数は、二項分布の累積成功確率が基準の値以上になる成功数のなかで、最小値を求めます。

（二項分布の累積した成功率が、ある基準の値以上になるときの、最小の成功数を計算します。）

この記事では、コイン投げを10回行って、表が出る回数を事例として、BINOM.INVのつかい方について説明します。

BINOM.INV 関数とは

BINOM.INV 関数は、二項分布の累積確率が基準の値以下になる成功数のなかで、最小値を求めます。

「＝BINOM.INV（試行回数, 成功率, 基準値）」

と入力します。これらの言葉について説明をすると、

二項分布とは

このBINOM.INV 関数をつかう前に、二項分布について確認しておきましょう。すでに理解されている方は読み飛ばしてください。

コイン投げで考えてみます。コイン投げをすると表が出る確率は1/2、裏が出る確率も1/2 です。

10回コイン投げをした結果はどうなるでしょうか。表が5回出て、裏が5回出ることもあれば、表が8回・裏が2回出るということもあります。

「10回コイン投げをすること」を何度か繰り返すと、

• 表が5回、裏が5回もあれば、
• 表が7回、裏が3回もあるし、はたまた
• 表が0回、裏が10回、なんでことも確率は小さいですが、ありえます。

表が出ることを「成功」とするなら、10回コイン投げをしたときに、成功数は5回になったり、7回になったり、0回になったりするわけです。

コイン投げで表が出る確率は1/2 なのですから、10回のコイン投げをすると、直観的に表が出るのは5回になることがいちばん多いだろうなとわかります。

10回のコイン投げをして、表が出る成功数が7回というのも、まあまあ発生するだろうとわかります。

10回のコイン投げをして、表が出る成功数が0回というと、めったにないだろうなとわかります。

それでは、いちばん多い、まあまあ多い、めったにない、というのは数値であらわすとどのくらいになるでしょうか。

それを示すのが、二項分布です。この例では、二項分布とは、10回のコイン投げという試行のうちで、表が出る回数（成功数）が従う確率分布のことです。

10回のコイン投げを行って、10回のうち

• 表が0回出る確率
• 表が1回出る確率
• 表が2回出る確率

…と、それぞれの確率を計算するには、

ｆ（ｘ）＝_ｎC_ｘ × ｐ^ｘ ×（１－ｐ）^ｎ-ｘ

の式で計算できます。表が0回出る確率から10回出る確率まで計算すると、次のようにまとまります。

• ｆ（0）＝₁₀C₀ × 0.5⁰ × 0.5¹⁰⁻⁰ ＝ 0.00098
• ｆ（1）＝₁₀C₁ × 0.5¹ × 0.5¹⁰⁻¹ ＝ 0.0098
• ｆ（2）＝₁₀C₂ × 0.5² × 0.5¹⁰⁻² ＝ 0.0439
• ｆ（3）＝₁₀C₃ × 0.5³ × 0.5¹⁰⁻³ ＝ 0.1172
• ｆ（4）＝₁₀C₄ × 0.5⁴ × 0.5¹⁰⁻⁴ ＝ 0.2051
• ｆ（5）＝₁₀C₅ × 0.5⁵ × 0.5¹⁰⁻⁵ ＝ 0.2461
• ｆ（6）＝₁₀C₆ × 0.5⁶ × 0.5¹⁰⁻⁶ ＝ 0.2051
• ｆ（7）＝₁₀C₇ × 0.5⁷ × 0.5¹⁰⁻⁷ ＝ 0.1172
• ｆ（8）＝₁₀C₈ × 0.5⁸ × 0.5¹⁰⁻⁸ ＝ 0.0439
• ｆ（9）＝₁₀C₉ × 0.5⁹ × 0.5¹⁰⁻⁹ ＝ 0.0098
• ｆ（10）＝₁₀C₁₀ × 0.5¹⁰ × 0.5¹⁰⁻¹⁰ ＝ 0.00098

で、これをグラフにすれば、二項分布のグラフができます。

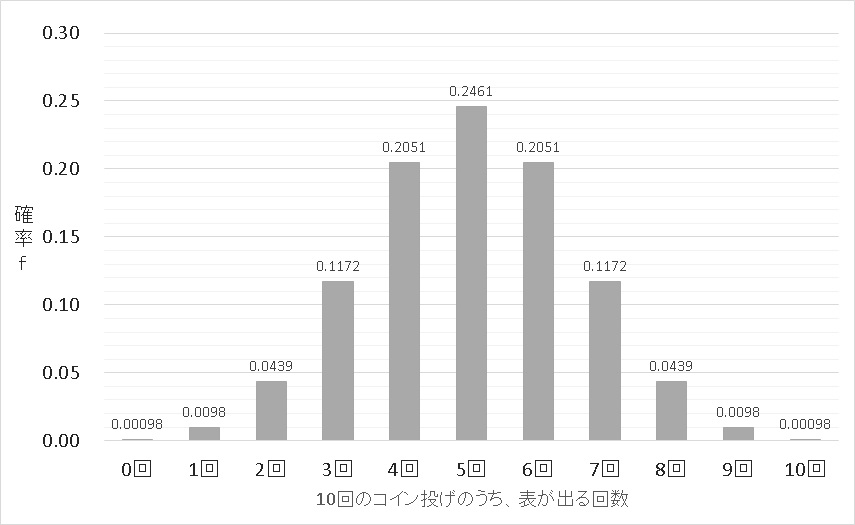
二項分布についてはこちらの記事を参考にしてください。

参考記事　ベルヌーイ試行と二項分布の違いと関係性

エクセルでの二項分布のつくりかたはこちら。

参考記事　エクセル関数BINOM.DISTによる二項分布の作り方

エクセルで、BINOM.DIST関数をつかうと次の表のように、10回のコイン投げを行って、10回のうち

• 表が0回出る確率
• 表が1回出る確率
• 表が2回出る確率

…と、それぞれの確率を計算をすることができます。

成功数	確率	累積確率
0	0.00098	0.00098
1	0.00977	0.01074
2	0.04395	0.05469
3	0.11719	0.17188
4	0.20508	0.37695
5	0.24609	0.62305
6	0.20508	0.82813
7	0.11719	0.94531
8	0.04395	0.98926
9	0.00977	0.99902
10	0.00098	1.00000

成功数5 回が0.24 で、いちばん成功確率が大きいです。

成功数0 回では、0.0098 でとても小さい確率ですね。

累積確率とは

• 表が0回出る確率
• 表が1回出る確率
• 表が2回出る確率

…を足し合わせていったものです。その成功数以下の成功確率の合計になります。

たとえば成功数3 回の成功確率は0.117 ですが、0 回から3 回の成功確率を合計した累積成功確率は0.171 です。

さて、ここでBINOM.INV 関数の話に戻ります。

BINOM.INV 関数での計算方法

コインを10回投げるときに、表が出たら成功であることとします。BINOM.INV 関数をつかうと、このときの、成功確率0.2 以上になるときの成功数は？という問いに答えることができます。

セルに

「＝BINOM.INV（　）」

を入力し、

「＝BINOM.INV（試行回数, 成功率, 基準値）」

試行回数、成功率、基準値を指定すると、計算されます。

10回のコイン投げでいえば、試行回数は10回です。成功率は、1/2です。

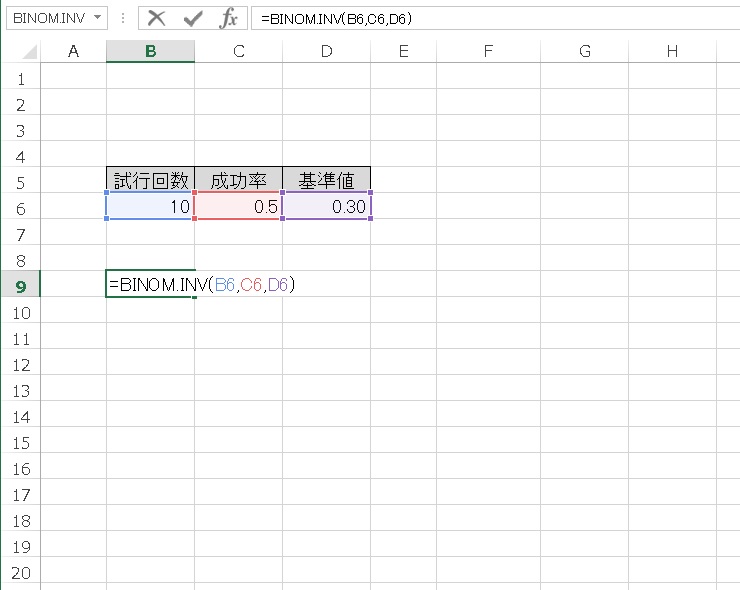
基準値は0.30 としてみます。

これで、表が出る確率の累積が、0.30 以上となるもっとも少ない成功数を計算できます。計算された成功数以上の成功数であれば、累積確率は0.30 以上あるよ、ということになります。

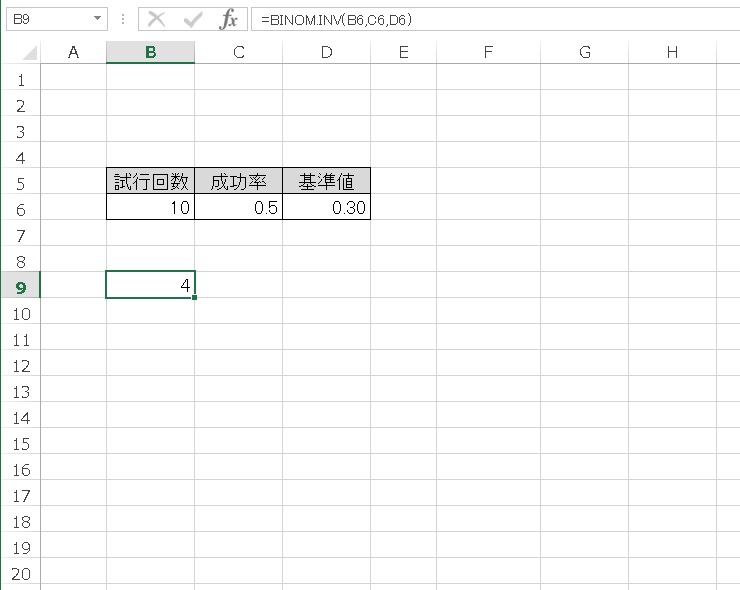
結果、4 回となりました。累積確率が、0.30 以上となる最小の成功数は、4 回です。

4 回の成功であれば、累積確率が0.30 以上となります。

各成功数ごとの確率と累積確率の表を見てもそうなっています。

成功数	確率	累積確率
0	0.00098	0.00098
1	0.00977	0.01074
2	0.04395	0.05469
3	0.11719	0.17188
4	0.20508	0.37695
5	0.24609	0.62305
6	0.20508	0.82813
7	0.11719	0.94531
8	0.04395	0.98926
9	0.00977	0.99902
10	0.00098	1.00000

では、基準値を0.80 にしてみましょう。

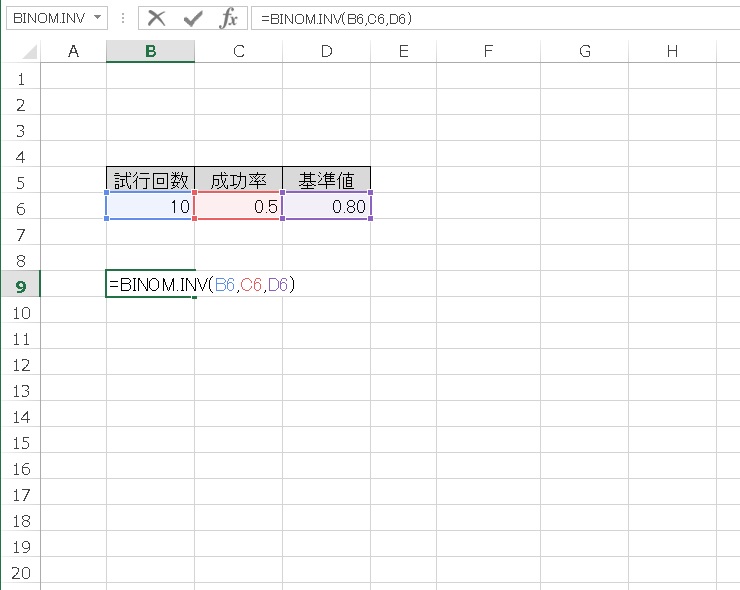
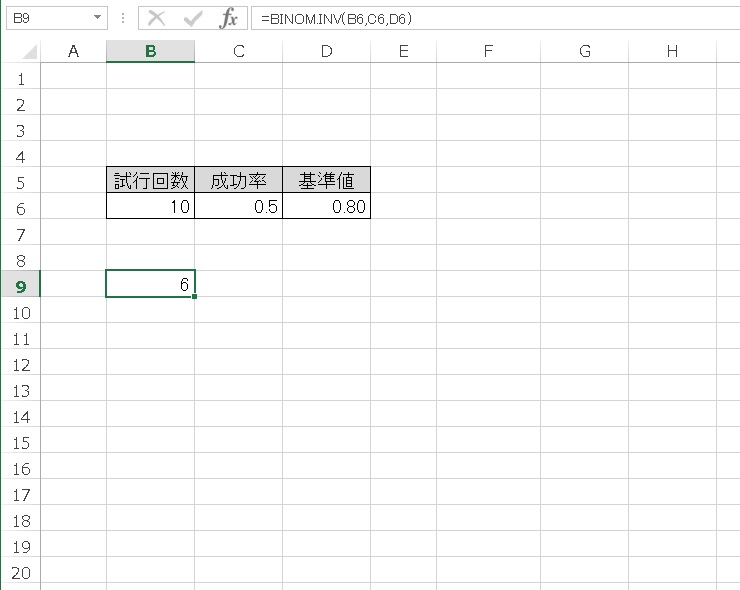
結果、6 回となりました。累積確率が0.80 以上となる最小の成功数は、6 回です。

6 回の成功であれば、累積確率が0.80 以上となります。