成功するか失敗するか一定の確率があるベルヌーイ試行を\(n\) 回行ったとき、何回成功するのかを示した分布が二項分布です。
参考記事 ベルヌーイ試行と二項分布の違いと関係性
成功確率\(p\) のベルヌーイ試行を\(n\) 回行うときに、ちょうど\(x\) 回成功する確率は次の式で計算できます。
$$f(x)=_n C_x \times p^x \times(1-p)^{n-x}$$
コイン投げを10回行って、表が出る回数が従う二項分布をつくるときには、
10回のコイン投げを行って、10回のうち
- 表が0回出る確率
- 表が1回出る確率
- 表が2回出る確率
…と、計算していくと次のようにまとまります。
$$f(0)=_{10} C_0 \times 0.5^0 \times(1-0.5)^{10-0}=0.00098$$
$$f(1)=_{10} C_1 \times 0.5^1 \times(1-0.5)^{10-1}=0.0098$$
$$f(2)=_{10} C_2 \times 0.5^2 \times(1-0.5)^{10-2}=0.0439$$
$$f(3)=_{10} C_3 \times 0.5^3 \times(1-0.5)^{10-3}=0.1172$$
$$f(4)=_{10} C_4 \times 0.5^4 \times(1-0.5)^{10-4}=0.2051$$
$$f(5)=_{10} C_5 \times 0.5^5 \times(1-0.5)^{10-5}=0.2461$$
$$f(6)=_{10} C_6 \times 0.5^6 \times(1-0.5)^{10-6}=0.2051$$
$$f(7)=_{10} C_7 \times 0.5^7 \times(1-0.5)^{10-7}=0.1172$$
$$f(8)=_{10} C_8 \times 0.5^8 \times(1-0.5)^{10-8}=0.0439$$
$$f(9)=_{10} C_9 \times 0.5^9 \times(1-0.5)^{10-9}=0.0098$$
$$f(10)=_{10} C_{10} \times 0.5^{10} \times(1-0.5)^{10-10}=0.00098$$
で、これをグラフにすれば下記のようになります。
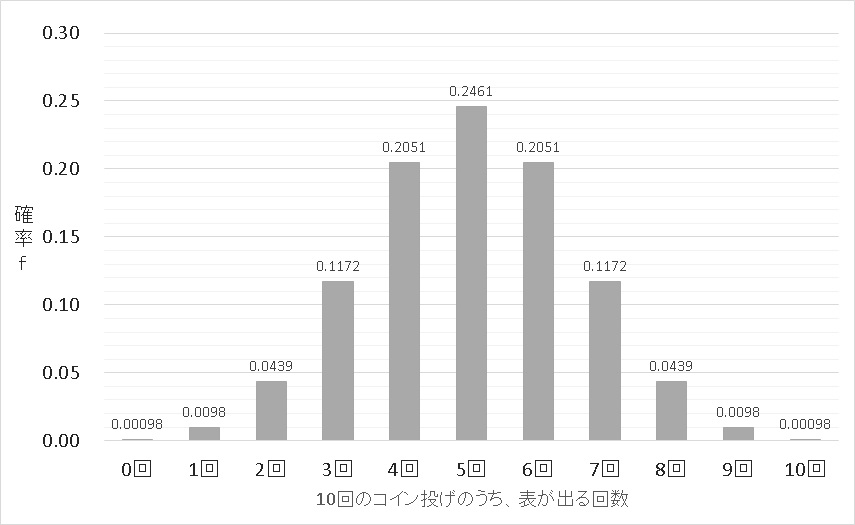
0回表が出る確率、1回表が出る確率…とそれぞれを計算していけばよいのですが、実際に行おうとすると、とても手間がかかってしまいます…。
$$f(x)=_n C_x \times p^x \times(1-p)^{n-x}$$
の数式をつかって計算して二項分布を求めていく場合、実際に自分で計算するのはとても大変ですよね。
しかし、エクセルの関数を使えば、簡単に計算することが可能です。
エクセルのBINOM.DIST 関数で計算する
使用する関数は、「=BINOM.DIST( )」です。
=BINOM.DIST(成功数、試行回数、成功率、関数形式)を指定します。
※二項分布は英語で、binomial distributionといいますから、それを略して、BINOMDIST です。
引き続き、10回のコイン投げを行って、表が出る回数についての二項分布を考えましょう。成功数は、表が出る回数です(表が出ることを成功である、とします)。
関数 BINOM.DIST の説明
成功数
成功数は、この場合では表が出る回数で、0回から10回までそれぞれ指定します。
試行回数
試行回数は、コイン投げの回数で、10回です。
成功率
成功率は、表が出る確率で、0.5です。
関数形式TRUE とFALSE の違い
関数形式は、累積分布関数はTRUE、確率質量関数はFALSE を指定します。この2つの違いは次のとおりです。
- TRUE 累積分布関数は、指定した成功数以下すべての発生確率の合計を表示します。
- FALSE 確率質量関数は、指定した成功数の発生確率を表示します。
10回のコイン投げでの成功数(表が出る回数)が5回であるときに、累積分布関数(TRUE)を選択すると、成功数0回になる確率、1回になる確率、2回なる確率、3回なる確率、4回なる確率、5回なる確率を足し合わせた数値となります。
セルにBINOM.DIST() を関数形式TRUE で入力
下記の画像のように、BINOM.DIST(成功数、試行回数、成功率、関数形式)を指定します。
ここでは、成功率0.5は直接入力し、試行回数は別のセルに入力してから、そのセルを選択しました。どちらでも大丈夫です。
それぞれの成功数(表が出る回数)の確率を見たいので、関数形式はFALSE(確率質量関数)にしました。
まず、成功数が0回になる確率を計算します。

成功数が0回になる確率が表示されました。

他のセルにもコピ―します。

このように計算できます。上記した、
$$f(x)=_n C_x \times p^x \times(1-p)^{n-x}$$
の式で計算した結果と同じになっていますね。
関数形式をTRUE(累積分布関数)の場合
関数形式をTRUE(累積分布関数)にして計算すると、指定した成功数以下すべての発生確率を合計した値が表示されます。

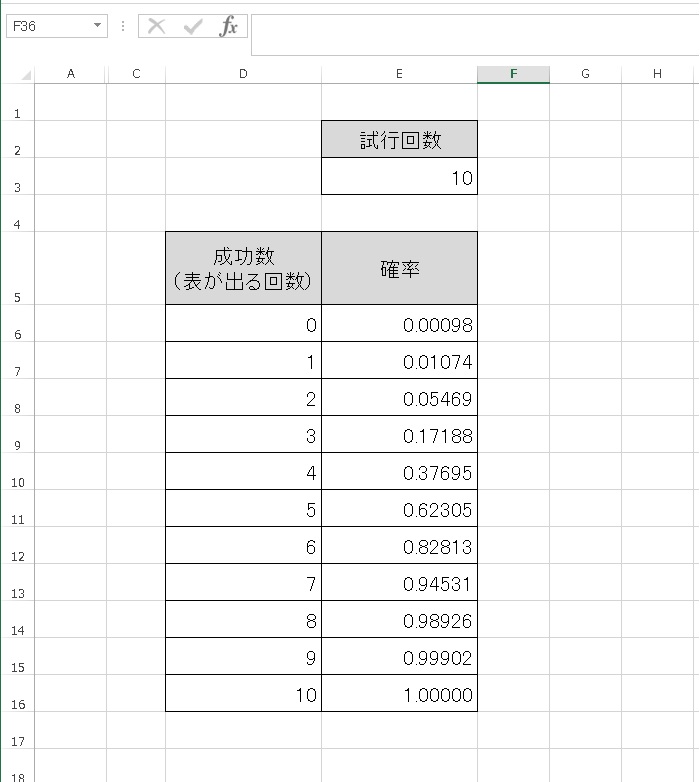
たとえば、成功数3 の行は、0.17188となっています。
TRUE(累積分布関数)ではなくて、FALSE(確率質量関数)で計算した場合は、
- 成功数0回・・・ 0.00098
- 成功数1回・・・ 0.00977
- 成功数2回・・・ 0.04395
- 成功数3回・・・ 0.11719
と表示されていました。それぞれの回数での確率です。
これらを合計すると、TRUE(累積分布関数)で計算したときの値と、同じ値になるはずです。
※ここでは、四捨五入によって小数点第5位までしか表示していないので、小数点第5位だけわずかに異なっています。