二項分布で、ある範囲の確率を計算するBINOM.DIST.RANGE 関数

2021/3/24 エクセル




BINOM.DIST.RANGE 関数は、二項分布で、成功数が、ある成功数と他の成功数の間の数値になる確率を計算します。

この関数を使用するときには、試行回数、成功率、基準値を入力します。

これらの言葉の意味は次のとおりです。

試行回数

全体の試行回数のことです。

※実験や観測を「試行（trial）」といいます。

 

成功率

事前にわかっている確率のことです。たとえば、コイン投げをして表が出る確率は、1/2 です。

 

基準値

累積した成功率が、ある基準の値以上になるときの、最小の成功数を計算しますが、この「ある基準」がこれに該当します。

二項分布とは

このBINOM.DIST.RANGE 関数をつかう前に、二項分布について確認しておきましょう。すでに理解されている方は読み飛ばしてください。

成功するか失敗するか一定の確率があるベルヌーイ試行を、n 回行ったとき、何回成功するのかを示した分布が、二項分布です。

参考記事　ベルヌーイ試行と二項分布の違いと関係性

ｎ回のベルヌーイ試行を行うときにちょうどｘ回成功する確率は次の式で計算できます。

ｆ（ｘ）＝ｎCｘ × ｐｘ ×（１－ｐ）ｎ-ｘ

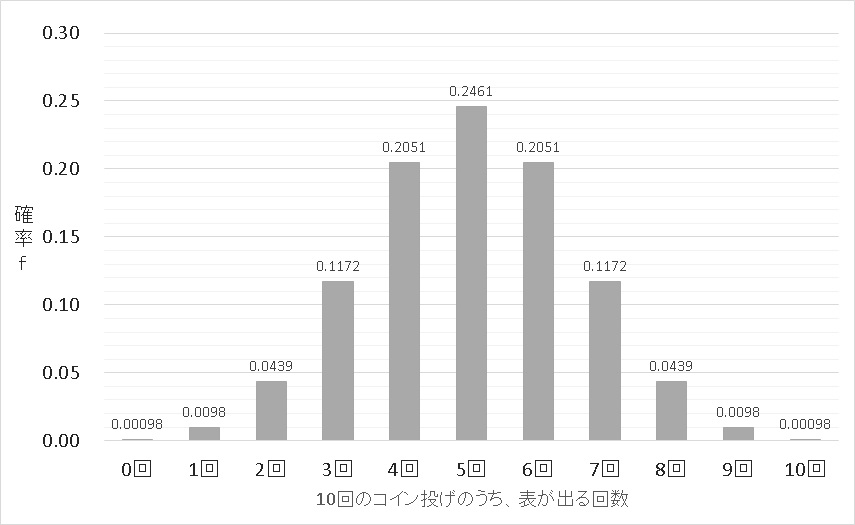
このコイン投げを10回行って、表が出る回数が従う二項分布をつくるときには、

10回のコイン投げを行って、10回のうち

  • 表が0回出る確率
  • 表が1回出る確率
  • 表が2回出る確率

…と、計算していくと次のようにまとまります。

  • ｆ（0）＝10C0 × 0.50 × 0.510−0 ＝ 0.00098
  • ｆ（1）＝10C1 × 0.51 × 0.510−1 ＝ 0.0098
  • ｆ（2）＝10C2 × 0.52 × 0.510−2 ＝ 0.0439
  • ｆ（3）＝10C3 × 0.53 × 0.510−3 ＝ 0.1172
  • ｆ（4）＝10C4 × 0.54 × 0.510−4 ＝ 0.2051
  • ｆ（5）＝10C5 × 0.55 × 0.510−5 ＝ 0.2461
  • ｆ（6）＝10C6 × 0.56 × 0.510−6 ＝ 0.2051
  • ｆ（7）＝10C7 × 0.57 × 0.510−7 ＝ 0.1172
  • ｆ（8）＝10C8 × 0.58 × 0.510−8 ＝ 0.0439
  • ｆ（9）＝10C9 × 0.59 × 0.510−9 ＝ 0.0098
  • ｆ（10）＝10C10 × 0.510 × 0.510−10 ＝ 0.00098

で、これをグラフにすれば下記のようになります。

BINOM.DIST.RANGE 関数で指定した範囲の確率を計算する

上記したように

ｎCｘ × Pｘ ×（１－P）ｎ-ｘ

の数式をつかって計算して二項分布を求めていく場合、実際に自分で計算するのはとても大変ですよね。

BINOM.DIST.RANGE 関数は、二項分布で、成功数が、ある成功数と他の成功数の間になる確率を計算します。

この例では、成功数はコイン投げで表が出る確率です。

セルに

「＝BINOM.DIST.RANGE（　）」

を入力し、

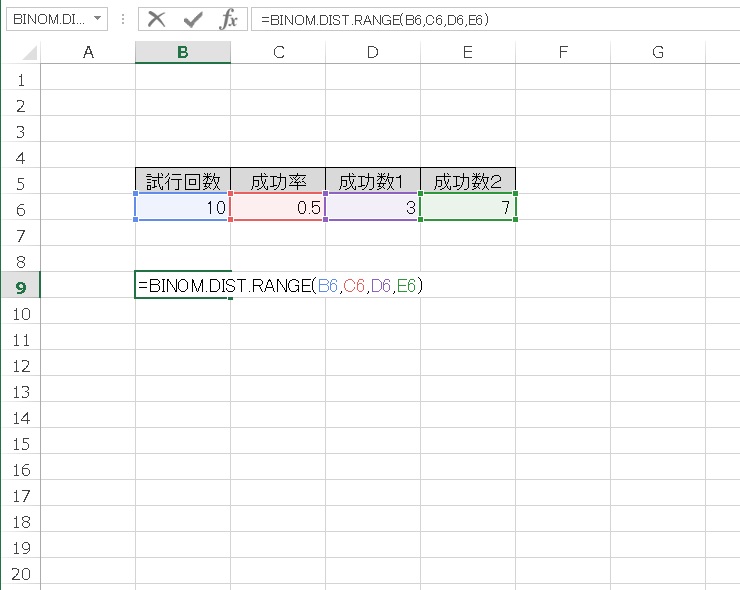
「＝BINOM.DIST.RANGE（試行回数、成功率、成功数①、成功数②）」

試行回数、成功率、成功数①、成功数②を指定すると、計算されます。

10回のコイン投げでいえば、試行回数は10回です。成功率は、1/2です。

成功数は3 回から7 回 とします。

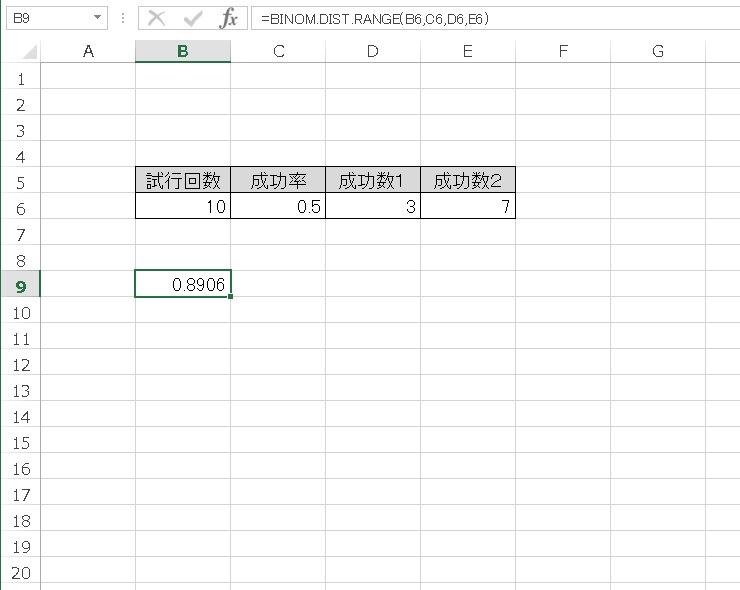
結果は、0.8906 となりました。

10回コイン投げをしたときの、各成功数ごとの確率を表にすると、こうなります。

成功数確率
00.00098
10.00977
20.04395
30.11719
40.20508
50.24609
60.20508
70.11719
80.04395
90.00977
100.00098

グラフにするとこうです。

成功数3 回から7 回の場合までの、それぞれの確率を足し合わると、0.8906 となりますね。

10回のコイン投げを行って表が出る回数（成功数）は、0.8906 の確率で、3 回から7 回の間になるということです。

成功数②を指定しないと、成功数が3 回のときの確率が計算されます。

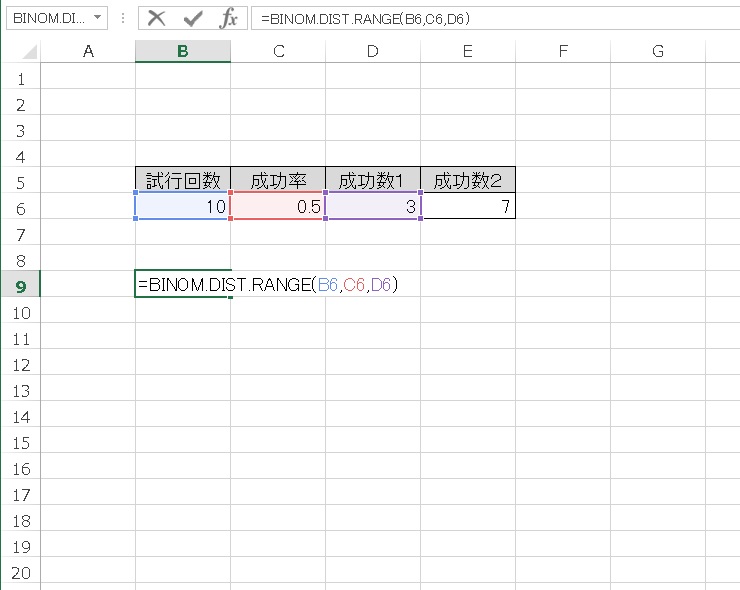
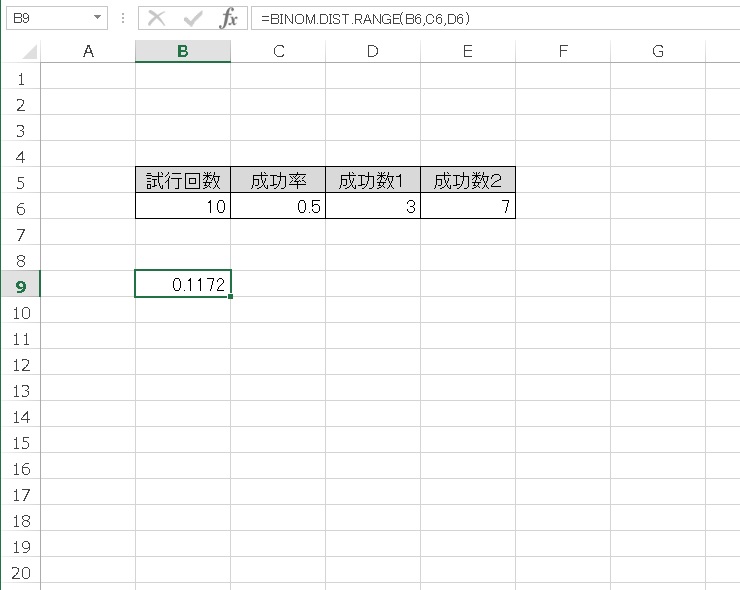
結果は、0.1172 となりました。上記の確率の表や、グラフで読める数値と同じです。