2つの量的データがあったとき、片方が大きくなれば、もう片方も大きくなる、あるいは小さくなるといったような関係性のことを相関関係といいます。
散布図を描いたり、相関係数を計算することで、数字で2つのデータの関係性をとらえることができます。
参考記事 散布図の作り方
参考記事 相関関係の意味と相関係数の計算方法
量的データを扱う場合はこれでいいのですが、質的データを扱う場合は、相関係数の計算はできません。
この記事では、名義尺度と間隔尺度のデータの場合の相関係数の計算について解説します。
名義尺度データと間隔尺度のデータであれば、相関比をつかって相関関係がどの程度なのか数値化します。
相関比とは
相関比とは、名義尺度データと間隔尺度のデータの相関関係の程度を数値化したものです。
会社で社員旅行の行き先のアンケートを例にして考えてみます。
旅行先としては、次の3つの候補がありました。
- 北海道
- 軽井沢
- ハワイ
どこに行きたいかアンケートをとってみると、年齢によって、旅行先の好みが分かれていそうでした。
| № | 年齢(才) | 行きたい場所 |
|---|---|---|
| 1 | 28 | ハワイ |
| 2 | 24 | ハワイ |
| 3 | 29 | 北海道 |
| 4 | 35 | 北海道 |
| 5 | 42 | 北海道 |
| 6 | 45 | 軽井沢 |
| 7 | 55 | 軽井沢 |
| 8 | 47 | 軽井沢 |
| 9 | 37 | 北海道 |
| 10 | 32 | ハワイ |
| 11 | 31 | 北海道 |
| 12 | 51 | 軽井沢 |
| 13 | 49 | 軽井沢 |
| 14 | 30 | ハワイ |
| 15 | 29 | ハワイ |
行き先事に年齢データをまとめると、
| 北海道 | 29、35、42、37、31 |
| 軽井沢 | 45、55、47、49、51 |
| ハワイ | 28、24、32、30、29 |
となりました。
平均をとると、
| 北海道 | 34.8 |
| 軽井沢 | 49.4 |
| ハワイ | 28.6 |
です。
年齢によって、好む旅行先が変ってくるのか。グラフをつくって見てみました。
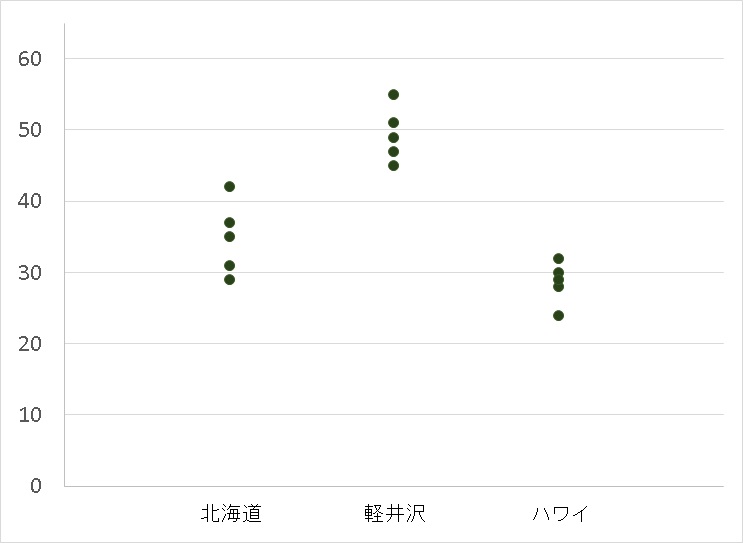
北海道を旅行先として好む年代、軽井沢を旅行先として好む年代、ハワイを旅行先としてこのむ年代には、違いがあるように見えますね。
- 北海道は30代~40代前半
- 軽井沢は40代から50代
- ハワイは20代~30代前半
から好まれるようですね。
これを数値で捉えるために、相関比があります。
相関比は、グループ内のバラつきと、グループ間のバラつきを見るものです。
グループ内での年齢のバラつきが小さくて、グループ間の年齢のバラつきが大きいほど、グループと年齢の関係は強いことになります。たとえば、ハワイは20代~30代前半の人に好まれていて、他のグループ(軽井沢、ハワイ)とは年齢幅がほとんど重複していません。これは、年齢層によって、好む旅行先が違っているということになります。
年齢層によって、好む旅行先が違っていないとしたら、グループ間のバラつきは無くなります。
たとえば、こんなふうになるはず。
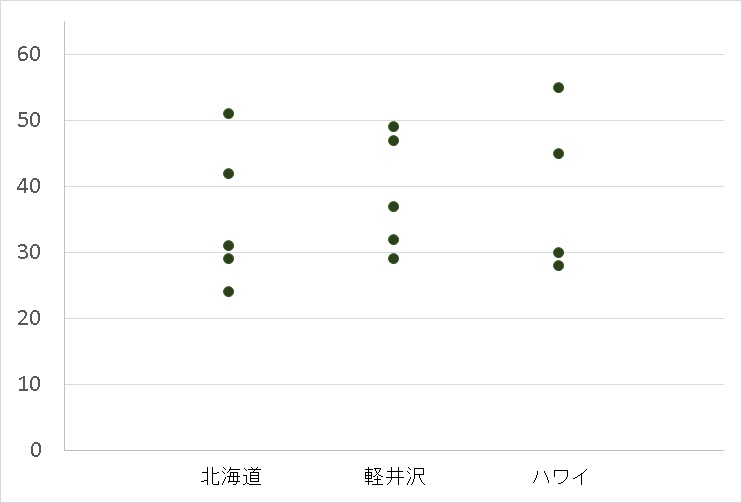
相関比を計算する
相関比の計算式
グループ内の変動を級内変動、グループとクループの間の変動を級間変動といって、これらを利用して、相関関係を数値化するのが、相関比です。
変動は、級内変動、級間変動に分けられます。級内変動と級間変動を足し合わせると、全変動になります。
相関比 = 級間変動 / 全変動
全変動 = 級間変動 + 級内変動
変動を記号Sであらわすと、
S = Sw + Sb
となります。
※wは、withinの頭文字、bは、betweenの頭文字。
級内変動を計算する
北海道グループ、軽井沢グループ、ハワイグループ、それぞれのグループの中での変動を計算します。
- グループ内の各データからグループの平均値を引く。すると偏差が得られる。
- 偏差を偏差を二乗する。
- すべて足し合わせる。
つまり偏差平方和を計算します。
軽井沢グループ、またハワイグループでもそれぞれ、偏差平方和を計算し、その3つを合計すると、級内変動となります。
級内変動 = 北海道グループの偏差平方和 + 軽井沢グループの偏差平方和 + ハワイグループの偏差平方和
北海道グループのデータをx、軽井沢グループのデータをy、ハワイグループのデータをzとします。
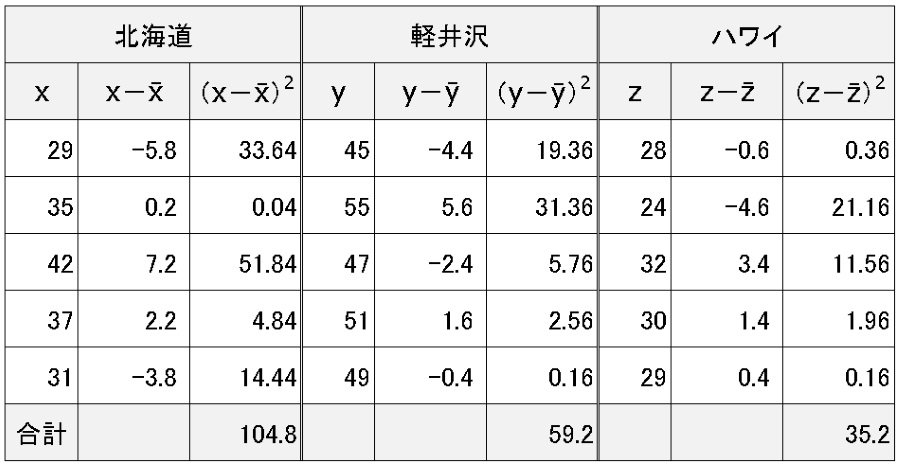
- 北海道のグループの級内変動は、104.8
- 軽井沢グループの級内変動は、59.2
- ハワイのグループの級内変動は、35.2
です。これらを合計すると、199.2 となります。
級内変動 = 199.2
です。
全変動を計算する
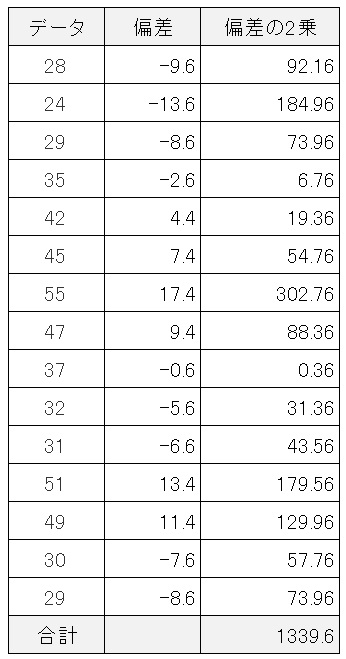
グループを分けずに考えて、すべてのデータの偏差の2乗を足し合わせます。
全データの偏差平方和です。
となりました。
級間変動/全変動 を計算する
全変動は、
全変動 = 級内変動 + 級間変動
ですから、1から\(\frac{級内変動}{全変動}\) を引けば、残りは\(\frac{級間変動}{全変動}\) であり、つまり相関比となります。
$$1-\frac{級内変動}{全変動}=\frac{級間変動}{全変動}$$
$$1-\frac{199.2}{1339.6}=\frac{1140.4}{1339.6}$$
$$相関比=0.85129$$
1 - 級内変動 / 全変動 = 級間変動 / 全変動
1 - 199.2 / 1339.6 = 1140.4 / 1339.6
相関比 ≒ 0.85
相関比 ≒ 0.85 となりました。