二つの変数があったときに、一方が増えると、もう一方も増えるといったように、連動する傾向がある関係のことを、相関関係といいます。
この記事では、“ペーパーテスト”と“仕事の実力”の相関関係を例にして、計算方法を解説します。
ペーパーテストと仕事の実力の関係
「ペーパーテストと仕事の実力は関係ない」と言われることもありますが、私は、関係あるだろうと思っています。とくに、ペーパーテストで問われることが、仕事で必要となることと一致していれば、そうなるはず。
ペーパーテストでは、知識の量、基礎的な計算能力や読解力などをはかることができます。結果がよければ、仕事でつかう知識があり、計算などの処理能力も速くて正確だということになります。
そういう人のほうが、仕事もできそうですね。
ある会社の経営者が、勉強によって知識を増やしてもらうのを狙いとして、従業員に対してペーパーテストを実施しました。
また、各従業員のテストの結果と仕事の実力・評価を見て、それらに関係があれば、定期的にテストを実施して勉強するように促したり、新たな人材の採用試験でペーパーテストを実施するのもいいのでないかと経営者は考えました。
テスト実施後に、得られたペーパーテストの結果と普段の仕事の実力・評価に関係があるのかを見てみました。
テストを受けた従業員は、Aさん、Bさん・・・Jさんの10人がいます。
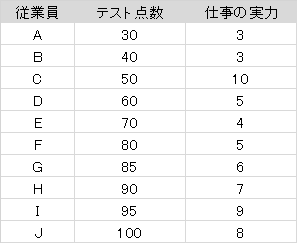
テストの結果と仕事の実力を一覧にし、合わせてテストの点数を横軸、仕事の実力・評価を縦軸として散布図を書いてみました。
散布図を見れば、2つの変数の関係性をパッと把握することができます。
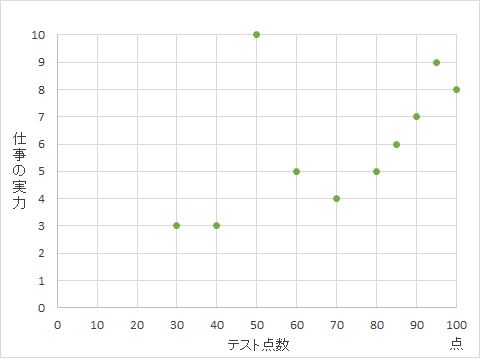
横軸がペーパーテストの点数、縦軸が仕事の実力です。
打点が右肩上がりになっていて、ペーパーテストの点数が高い人ほど、仕事の実力も高い人が多いように見えます。
テストの点数で80点以上の高得点をとっている人は仕事の実力も比較的良く、テストの点数が30点、40点と悪い人は仕事の実力もないようです。ただし、テストの点数は50点なのに、仕事の実力がずば抜けている人が1人いることがわかります。
散布図では、ペーパーテスト点数が増加すると、仕事の実力も増える関係にあるとしたら、 右肩上がりに打点されます。
このように\(x\)が増えると\(y\)も増えるというように、\(x\)と\(y\)の値に連動する傾向があるとき、「\(x\)と\(y\)の値の間には相関がある」といいます。
- \(x\)が大きくなるにしたがって、\(y\)も大きくなる傾向を「正の相関」
- \(x\)が大きくなるにしたがって、\(y\)が小さくなる傾向を「負の相関」
といいます。これが相関関係です。
逆の動きでは、
- \(x\)が小さくなるにしたがって、\(y\)も小さくなる傾向を「正の相関」
- \(x\)が小さくなるにしたがって、\(y\)は大きくなる傾向を「負の相関」
といいます。
散布図を見れば、ペーパーテストの点数が高い人ほど仕事の実力もあることがなんとなくわかりますが、 何かはっきりとした数値が欲しいものです。
こんなときに使える指標として相関係数があります。
相関係数は2つのものごとの関係性を数値で把握することできるものです。
相関係数にはいくつかの種類がありますが、ふつう、相関係数というとピアソンの積率相関係数のことを指します。この記事で説明しているのは、ピアソンの積率相関係数であり、単に相関係数と書いています。
相関係数は「r」の記号であらわし、計算式はこのようになります。
また言葉で書くとこのようになります。
$$r=\frac{xとyの偏差積和}{\sqrt{xの偏差平方和}\times\sqrt{yの偏差平方和}}$$
また、こちらの式でもよいです。
$$r=\frac{\frac{1}{n}\sum_{i=1}^n (x_i -\bar{x})(y_i -\bar{y})}{\sqrt{\frac{1}{n}\sum_{i=1}^n (x_i -\bar{x})^2}\times\sqrt{\frac{1}{n}\sum_{i=1}^n (y_i -\bar{y})^2}}$$
$$r=\frac{xとyの共分散}{xの標準偏差\times yの標準偏差}$$
一番簡単に式であらわすとしたら、\(x\)と\(y\)の共分散を\(S_xy\)、\(x\)の標準偏差を\(S_x\)、\(y\)の標準偏差を\(S_y\)として、
$$r=\frac{S_{xy}}{S_x\times S_y}$$
です。
偏差積和とはまず、データから平均値を引いたものが偏差。2つの変数\(x\)と\(y\)があったときに、\(x\)の偏差と\(y\)の偏差を掛けたものが、偏差積です。
そして、各データの偏差積を足し合わせたものが、偏差積和です。
偏差平方和とは
変数\(x\)があったときに、変数\(x\)の偏差を二乗し、すべて足し合わせたものが偏差平方和です。
参考記事 偏差平方和と分散、偏差積和と共分散
相関係数は、かならず +1 ~ 0 ~-1 の範囲の値をとります。値が大きくて+1 に近いほど、強い正の相関があり、0に近いと相関はなく、値が小さくて-1 に近いほど強い負の相関となります。
相関係数の計算方法
上に掲載した表のデータから、”テストの点数”と“仕事の実力”相関係数を計算していきましょう。

簡単な流れとしては、
テストの点数\(x\)、仕事の実力を\(y\)としたら、
■偏差積和のを計算する
- \(x\)から\(\bar{x}\)を引いて、偏差を求める
- \(y\)から\(\bar{y}\)を引いて、偏差を求める
- \(x\)の偏差と\(y\)の偏差を掛けて偏差積を求める
- 全データの偏差積を足し合わせる
■\(x\)の偏差平方和を求める
- \(x\)から\(\bar{x}\)を引いて、偏差を求める
- 偏差を二乗して、偏差平方を求める
- 全データの偏差平方を足し合わせて、偏差平方和を求める
■\(y\)の偏差平方和を求める
- \(y\)から\(\bar{y}\)を引いて、偏差を求める
- 偏差を二乗して、偏差平方を求める
- 全データの偏差平方を足し合わせて、偏差平方和を求める
そして、\(x\)と\(y\)偏差積和、\(x\)の偏差平方和、\(y\)の偏差平方和の3つを数式に当てはめればOKです。
それでは、
- \(x\)の偏差、偏差平方、偏差平方和
- \(y\)の偏差、偏差平方、偏差平方和
- \(x\)と\(y\)の偏差積、偏差積和
を表にまとめましたので、こちらをつかって計算します。

$$=\frac{285}{\sqrt{5250}×\sqrt{54}}$$
$$=\frac{285}{72.46×7.348}$$
$$=0.535$$
テストの点数と仕事の実力の相関係数を計算すると、0.535となりました。
0.535は、まあ相関があるかなと判断できる数値です。
上に書きましたが、相関係数は、+1 ~ 0 ~-1 の範囲にある数値となります。値が+1 に近づくほど強い正の相関があり、0に近いと相関は無し、-1 に近づくほど強い負の相関となります。
下記の記事で、相関関係が強いか弱いかを判断するための目安を書いていますので、もしよろしければ読んでみてください。
参考記事 相関係数の強い・弱いの目安
コメント
誤読する人はいないと思いますが
> 下記の式でも同じ結果がでます。
の下にある式の分母の /n の部分は ルートの中にないといけませんね。
ご指摘ありがとうございます。
読み返して確認、修正いたします。