COVARIANCE 関数は、2 組の対応するデータ間の共分散を計算することができる関数です。
「CO」が「共に」の意味、「VARIANCE」は「分散」の意味で、合わせてCOVARIANCE「共分散」です。
共分散とは
共分散とは、2 組の対応するデータ間の関係を示した数値です。2 組の対応するデータというと、たとえば、人の身長と体重、気温とビールの売上といったデータがあります。
偏差と偏差積和と合わせて説明します。
- 偏差とは、各データから平均値を引いたもの。
- 偏差積とは、対応するxとyのデータがあったときに、それぞれのxの偏差、yの偏差を掛け合わせたもの。
- 偏差積和とは、それぞれxとyの偏差積を足し合わせたもの。
- 共分散は、偏差積和を組数nで割ったものです。共分散は、偏差積の平均値ということになります。
下記の記事で説明をしていますので参考にしてください。
参考記事 偏差平方和と分散、偏差積和と共分散
COVARIANCE.S 関数とCOVARIANCE.P 関数の違い
共分散を計算する関数には、「COVARIANCE.S」と「COVARIANCE.P」の2種類があります。
2つの違いは、
- 「COVARIANCE.S」はデータを標本とみなして計算をする。
- 「COVARIANCE.P」はデータを母集団とみなして計算をする。
です。
参考記事 母集団と標本の意味とその違い
参考記事 共分散を計算する関数COVARIANCE.PとCOVARIANCE.Sの違い
COVARIANCE 関数をつかった共分散の計算方法
ここに、とある10人の身長と体重のデータがあります。これらの身長データと体重データの共分散を、COVARIENCE.S 関数で計算してみましょう。
ここでは、COVARIANCE.S 関数をつかっておきます。とくにデータ数が少ない場合、おおむね30個未満のときには、COVARIANCE.S 関数をつかったほうがよいです。
データ数が多い場合は、S のほうでも、P のほうでも、計算結果はほとんど変わらなくなりますから、どちらをつかってもよくなります。
セルに
「=COVARIANCE.S( )」
を入力し、
「=COVARIANCE.S(配列①, 配列②)」
対応した配列を指定すると、共分散が計算されが、表示されます。
- 配列①と配列②に入力されているデータの数は、同じにします。データ数が異なっていると、エラー値「#N/A」が表示されます。
- 文字列、論理値、空白のセルがある場合は、これらは無視されて計算されます。
- また、データが入力されていない場合、1組のデータしか入力されていない場合も、エラー値となり、「#DIV/0!」が表示されます。
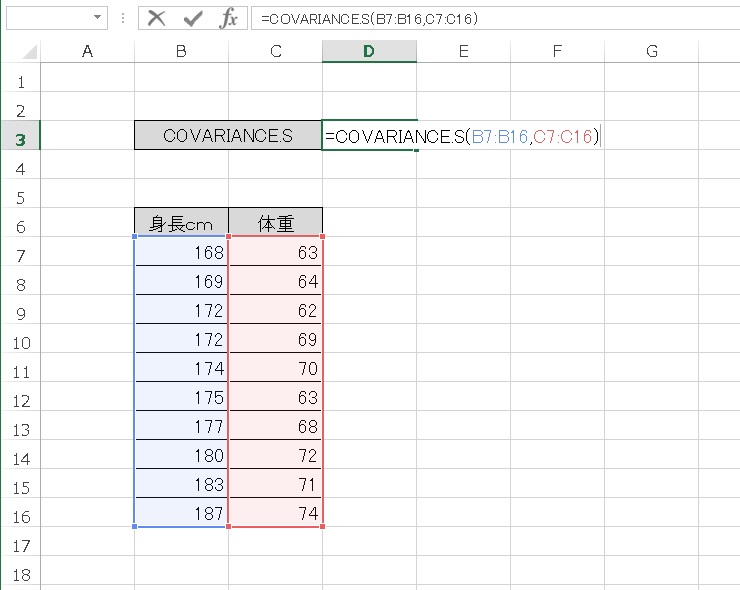

共分散は、21.20 となりました。