エクセルで共分散を計算する関数として、COVARIANCE.P とCOVARIANCE.S の2つがあります。両方とも共分散を計算する関数なのですが、お尻についた「P」と「S」の違いはなんなんでしょうか?
COVARIENCE.P とCOVARIENCE.Sの違い
COVARIANCE.Pは、母集団の共分散を計算します。母集団のデータが100個あって、その100個をすべて得て、共分散を求めるのであれば、こちらを使います。
COVARIANCE.Sは、母集団から抜き取った標本の共分散を計算する場合です。
母集団と標本の意味については、こちらの記事に書いています。
参考記事 母集団と標本の意味とその違い
共分散の計算手順としては、まず、各データxとyの偏差を計算し、それらを足し合わせまます。その後、データ数で割って共分散を求めるわけです。
エクセルでCOVARIENCE.P(S)関数を使った計算方法
COVARIENCE.S 関数を使う場合
COVARIENCE.S 関数をつかうのは、計算につかうデータが標本データの場合です。
メーカーでとある製品を毎日毎日つくり続けているとします。30個ぶん、この製品のサイズ・重量をはかって、それらの共分散を計算するときのことを考えてみましょう。
メーカは、この製品をずっとつくり続けてきており、これからもつくり続けます。
ある日、30個だけのサイズと重量をはかるといっても、その30個についてだけを知りたいのではありません。ずっとつくり続けている製品すべてのサイズ・重量について知りたいのです。
そのような調査対象全体のことを母集団といいます。
過去から未来にかけてのすべての製品が母集団となるでしょう。こういった、数は無限であると考えられる母集団は、無限母集団といいます。
製品30個は、その無限母集団から取り出した一部分であり、これが標本です。
この場合に、共分散を計算するとしら、COVARIANCE.S をつかいます。
COVARIANCE.S の「S」は、sample(標本)の「S」で、英語で言うと母集団はpopulationです。COVARIANCE.P の「P」は population の「P」でしょう。
標本のデータで計算するならCOVARIANCE.S を使い、母集団全体のデータで計算するならCOVARIANCE.P を使います。
標本データから計算した共分散は、母集団の共分散よりも小さくなる傾向があります。
データからそのまま共分散を計算するのが、COVARIENCE.P 関数ですが、それで計算すると、ほんとうに知りたいと思っている母集団の共分散から、小さい方にズレが出やすくなります。
標本のデータをつかって共分散を求めるときでも、私たちが知りたいのは、母集団の共分散のはずです。
COVARIANCE.P 関数よりも、COVARIANCE.S 関数をつかったほうが、計算された共分散の値が大きくなるようになってますから、これによって、補正をする意味合いがあります。
COVARIANCE.S 関数で、母集団の共分散を推定することになります。
COVARIENCE.P 関数を使う場合
一方で、COVARIENCE.P 関数をつかうのは、計算につかうデータが母集団全体のデータの場合です。
ある高校で学生300人分の身長・体重を測定したとします。この300人のデータの特性を知りたいという考えであれば、母集団が300人だということになります。
得られたデータが母集団全体のデータであるときには、COVARIANCE.P 関数をつかいます。
データ数が多ければ、PとS、どちらを使ってもいい
ふつう、なにかの調査のためにデータを集めるときには、母集団すべてのデータを集められることは少ないです。標本を集めて、母集団の特性を推定することが多いでしょう。
となると、それは標本ですから、COVARIANCE.S 関数を選ぶ場面のほうが多いでしょう。
でも、データ数が多くなればなるほど、結局どちらをつかってもよくなります。
とある10人の身長と体重のデータがあります。この共分散をCOVARIENCE.S 関数、COVARIANCE.P 関数で計算してみましょう。

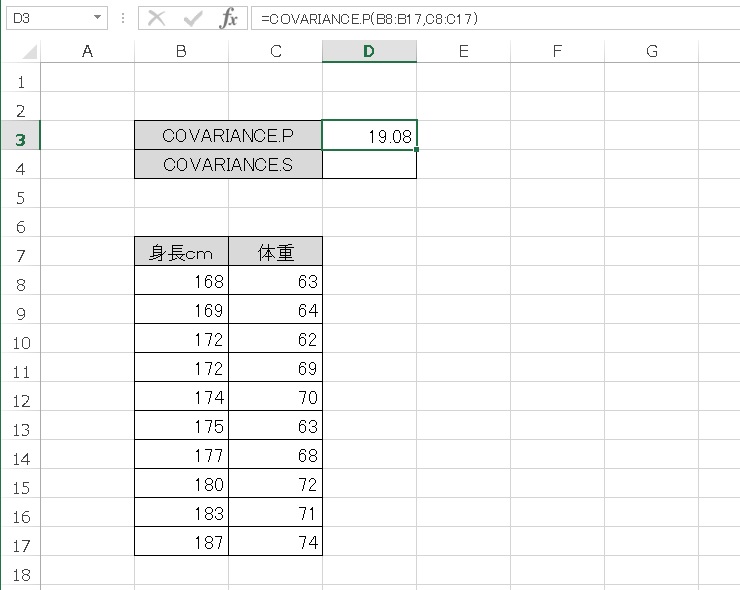

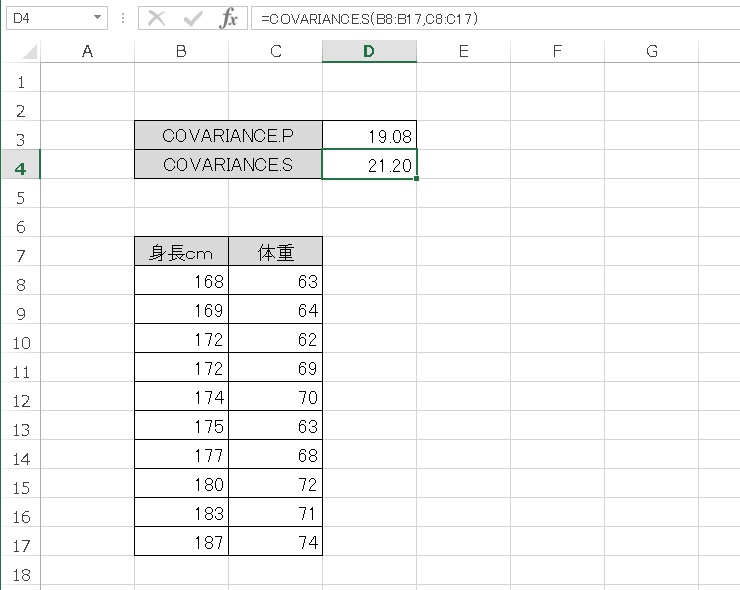
- COVARIANCE.P → 19.08
- COVARIANCE.S → 21.20
COVARIENCE.P のほうが小さい値になりました。
データ数を増やして100人の身長・体重データ(エクセルでランダムにつくったデータ)で計算すると、データ掲載は割愛しますが、
- COVARIANCE.P → 47.3484
- COVARIANCE.S → 47.8266
となりました。0.5程度の差しかありませんね。さらにデータが増えれば、ほとんど差がなくなっていきます。
厳密には、COVARIANCE.P とCOVARIANCE.S で計算結果の数値は違っているわけですが、わずかな数値の違いなので、データ数が多い場合は、どちらをつかってもいいかと思います。
ただし、標本のデータ個数がほんとうに少ないときに、共分散を計算する場合は、COVARIENCE.Sをつかったほうがよいという話です。