尖度とは
分布の尖り度合いを示すものが「尖度」です。
尖度は、
$$尖度=\frac{E[(X-μ)^4]}{\sigma^4}$$
で計算することができます。\(\frac{X-μ}{\sigma}\)を4乗した値の平均値です。
尖度の値が大きいほど尖った分布をしていることになります。
\(z\) 値(平均が0、標準偏差が1 の標準化したもの)=\(\frac{X-μ}{\sigma}\) を4乗した値の平均が、尖度の値となります。
正規分布の場合、尖度 = 3 となるので、これが基準となります。
- 「尖度-3 」が、0 より大きくなるのであれば(尖度-3 > 0 )、尖りが急で裾が長い分布
- 「尖度-3 」が、0 より小さくなるのであれば(尖度-3 < 0 )、尖りが丸く緩やかな山の形をした分布
となります。
エクセルKURT 関数での尖度の計算方法
尖度は、エクセルのKURT関数で求めることができます。
エクセルのヘルプには、KURT 関数の式は次のように掲載されています。
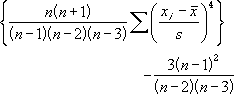
とある工場で製品の重量データをとってみると、次のようなデータが得られたとしましょう。
85、85、87、86、84、85、84、86、89、87、87、86、81、80、86、86、86、84、85、84、84、85、84、87、85、84、86、85、85、85、85、84、86、84、87、89、88、84、84、88、83、84、84、85、84、85、85、85、83、85、83、81、79、84、85、85、85、84、82、83、83、84、85、84、86、84、83、86、84、83、80、82、83、85、83、85、85、83、85、86、85、84、83、90、88、84、82、86、82、86、82、84、83、87、85、84、83、82、84、83、84、86、81、81、76、77、78、91、92、93、94
グラフにすると、左右の裾が長く、中央が尖った分布となりました。
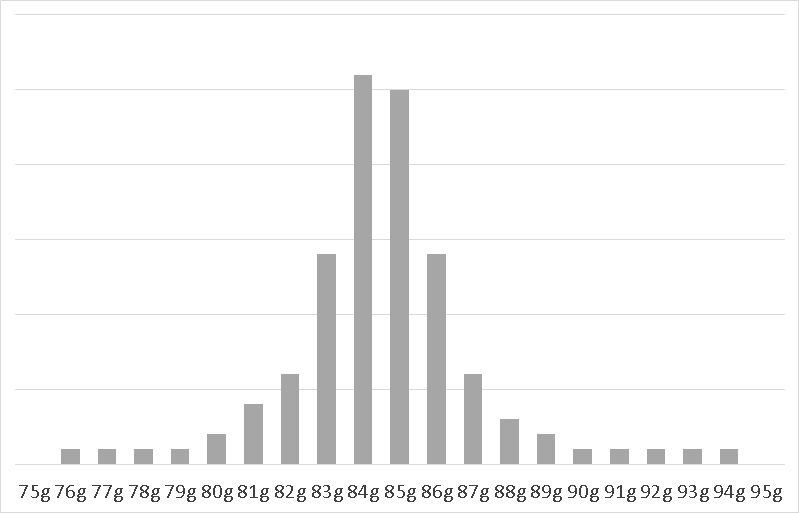
エクセルで計算するには、セルに
「=KURT( )」
を入力し、
「=KURT(データ範囲)」
データ範囲を指定してあげると、歪度が表示されます。
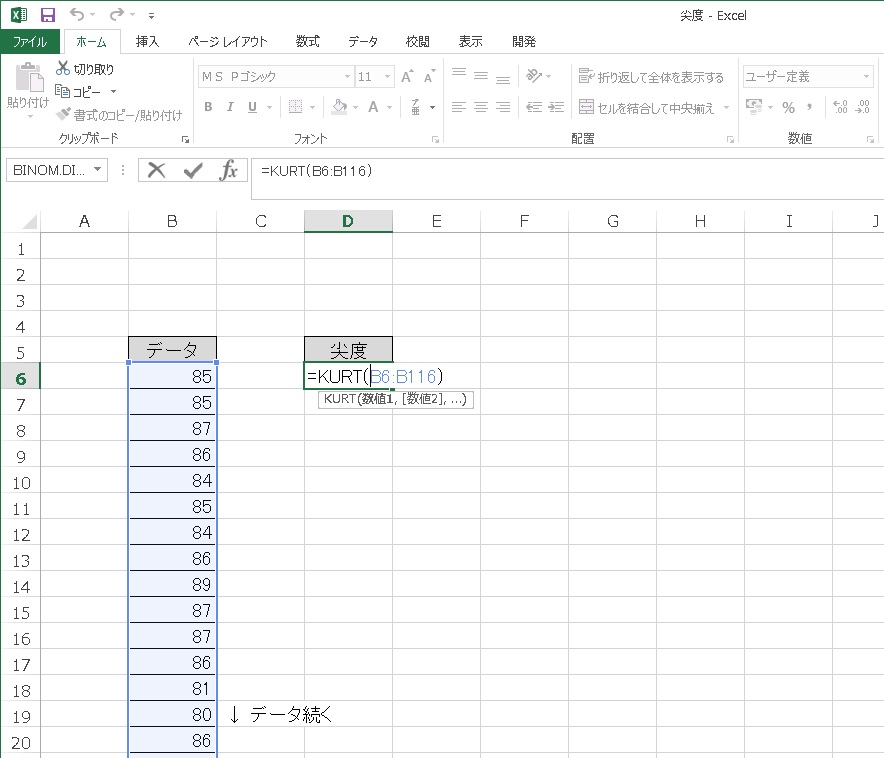
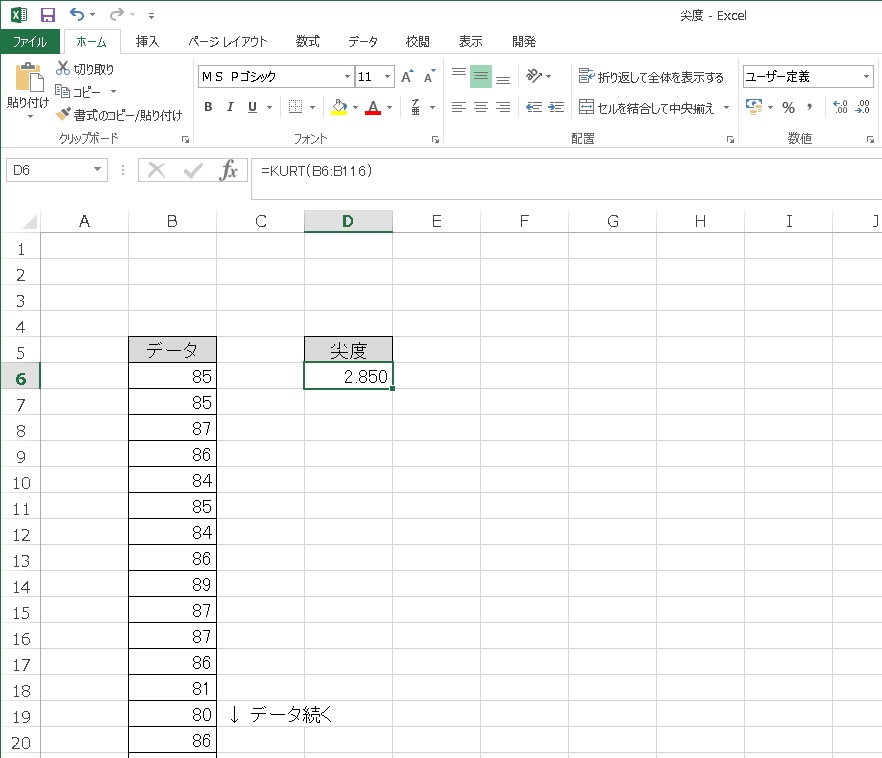
このデータを計算してみると尖度は、尖度-3 = 2.850になりました。
左右の裾が長く、中央部分が高く尖った分布なので、尖度の値が大きくなりました。