分布の形状を見るときに利用されるものとして、尖度があります。
尖度とは
「尖度」とは、文字通り、分布の尖り度合いを示すものです。
$$尖度=\frac{E[(X-μ)^4]}{\sigma^4}$$
これを尖度といって、尖度が大きいほど尖った分布をしていることになります。
\(z\) 値(平均が0、標準偏差が1 の標準化したもの)の\(\frac{X-μ}{\sigma}\) を4乗した値の平均が、尖度の値となります。
正規分布の場合、尖度 = 3 となるので、これが基準となります。
- 「尖度-3 」が0 より大きくなるのであれば(尖度-3 > 0 )、尖りが急で裾が長い分布
- 「尖度-3」 が0 より小さくなるのであれば(尖度-3 < 0 )、尖りが丸く緩やかな山の形をした分布
となります。
なぜ4乗で計算した結果が尖がり度合いを示すことになるのか
尖度は、なぜこのように4乗して計算し、0を越えると右の裾が長い分布、0より小さいと左の裾が長い分布を示すことなるのでしょうか。
4乗をすることによって、\(z\) 値=\(\frac{X-μ}{\sigma}\)の値が平均がから離れているほど、大きな値になりやすいです。
| \(\frac{X-μ}{\sigma}\) | 4乗の結果 |
|---|---|
| 0.1 | 0.14 = 0.0001 |
| 0.5 | 0.54 = 0.0625 |
| 1 | 14 = 1 |
| 1.25 | 1.254 = 2.4414 |
| 1.5 | 1.54 = 5.0625 |
| 1.75 | 1.754 = 9.3789 |
| 2 | 24 = 16 |
| 3 | 34 = 81 |
といったように、\(z\) 値=\(\frac{X-μ}{\sigma}\) の値が少し増えただけでも、4乗すれば大きな値になりやすいのです。
\(z\) 値の4乗=\((\frac{X-μ}{\sigma})^4\) の平均である尖度は、
中心に分布がたくさんあり、標準偏差は大きくなくて、裾が長く伸びた分布であると、中心から離れた箇所からの大きな影響があって、尖度の値を大きくします。
裾がぐいーんと長くて、中心が高くとんがっているほど、尖度は大きくなります。
緩やかな山の分布であれば、標準偏差が大きい分、\((\frac{X-μ}{\sigma})^4\) の値が大きくなりにくいです。
どんなグラフが、どんな尖度になるか
次のグラフは、正規分布に近い形の分布です。この尖度を、エクセル関数KURTで調べると、尖度-3 = -0.082 でした。
エクセルのヘルプには、KURT 関数の式は次のように掲載されています。
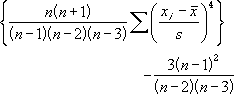
■尖度-3 = -0.082
正規分布に近い分布であったので、尖度-3 = 0 に近くなりました。
平均84.5g、標準偏差2.1gです。
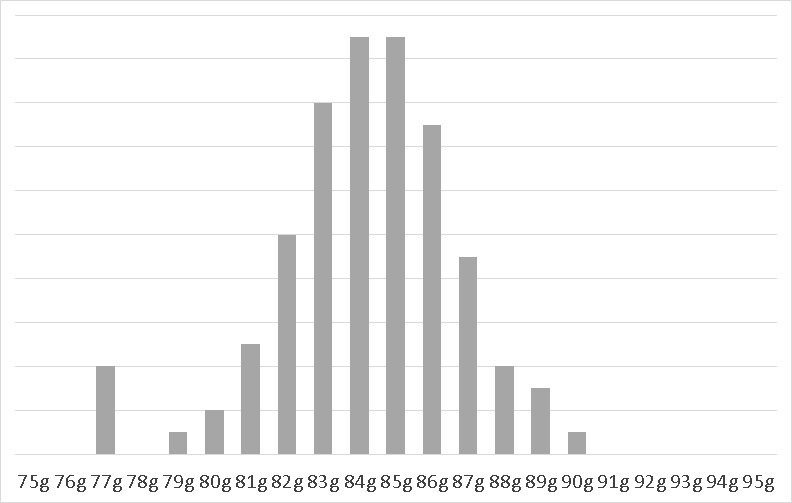
次は、裾を長くして中央部をより尖がるようにした分布です。エクセルのKURT 関数で調べると、尖度-3 = 0.834 でした。
■尖度-3 = 0.834

平均84.5g、標準偏差1.9gです
次は、さらに、裾を長くして中央部をより尖がるようにした分布です。エクセルのKURT 関数で調べると、尖度-3 = 2.850 でした。
■尖度-3 = 2.850

平均84.5g、標準偏差2.7gです。ひとつ上の分布グラフよりも、標準偏差は大きくなるのですが、端のほうにあるデータの4乗が効いて、尖度が大きくなるということでしょう。
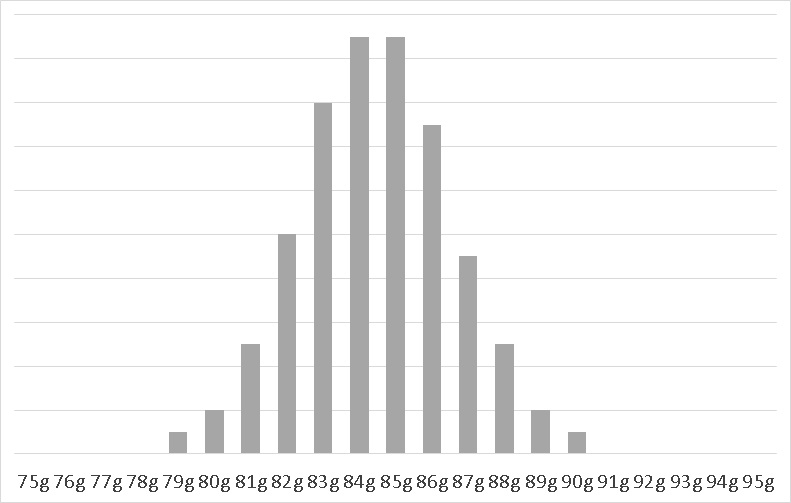
こんどは、逆に緩やかな分布です。
■尖度-3 = -0.610
緩やかな分布ですので、尖度-3 = -0.610 でした。正規分布だと 尖度-3 = 0 となりますから、正規分布よりも尖りがないことになります。
この分布は、平均 84.8g、標準偏差σ 4.1gでした。ほとんどのデータが2σの範囲に入ることになります。 中心から遠く離れた$z$値=$\frac{X-μ}{\sigma}$ が少ないということでしょう。
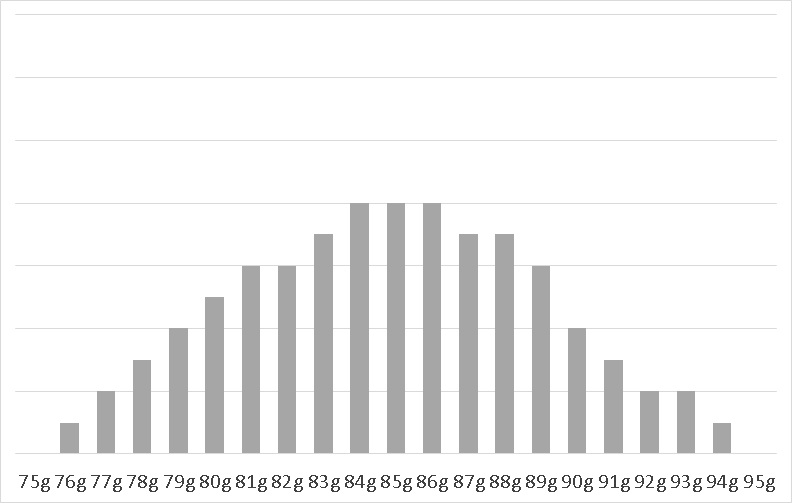
次は、上に掲載した尖度-3 = -0.082 の分布に、77gのデータをいくつか加えてみた分です。尖度は大きくなりました。
■尖度-3 = 1.051
分布の裾が伸びているわけではなく、外れ値の影響であっても、尖度は変わってしまいます。