大学の受験勉強をするときには、誰もが気にする偏差値。この偏差値も統計学的な計算によって出されます。
偏差値とはどのようなものなのか、偏差値はどのように計算するのかを書きました。
まず最初に基準化変量について、次に偏差値について解説します。
偏差値の計算式
偏差値の計算式だけを先に書きます。
\(50+\frac{自分の点数-平均点}{標準偏差}\times10\)
偏差値でわかるのは、相対的な自分の位置
受験勉強は勉強は自分との闘いであると考えて、できることを増やし、前回よりも点数を上げていくことが大事ですよね。
しかしながら、受験は競争ですから、大勢の受験生の中での自分のレベルを知ること、自分の点数の相対的な評価を知ることも必要です。
偏差値によって、相対的な自分の位置を知ることができます。周りの受験生のなかでは、上位にいるのか、それとも下位にいるのかといったことがわかります。
たとえば、自分がテスト受けて、点数が80点であったとしましょう。
このとき、仮平均点が70点であったら、自分がとった80点は良い点数となりますし、平均点が90点であったら、自分がとった80点は良い点数とはいえませんね。
また、自分の点数が80点で、平均点が70点であっても、
- 他の学生の点数が70点あたりに集中していて、80点以上をとった学生が少ない場合
- 80点をとった学生は多く、90点をとっている学生もいて、点数のばらつき範囲が広い場合
この二つの場合で、80点の評価が変わってきます。
つまり、平均点と点数のばらつきによって、80点の評価は変わるのです。ばらつきは、標準偏差という数値で示しますから、平均と標準偏差によって、自分の点数の相対的な評価が変わってくるということ。
そして、平均と標準偏差によって計算されるのが、偏差値なのです。
自分のテストの点数を、集団の中での位置関係でみて相対的に評価するために偏差値が活用されます。
参考記事 分散と標準偏差の意味と計算方法
偏差値の計算方法
偏差値の計算の流れを説明していきます。
偏差を計算する
まず、自分の点数から平均点を引いて偏差を計算します。
$$偏差=自分の点数-平均点$$
偏差が標準偏差 何個分なのかを計算する
自分の点数の偏差を標準偏差1単位あたりの偏差に変換します。
平均値を標準偏差で割って、偏差が標準偏差 何個分なのかを見るのですね。
$$\frac{自分の点数-平均点}{標準偏差}$$
これを「基準化変換」といいます。その標準偏差1単位あたりの偏差を「基準化変量」といいます。言い換えると、偏差が平均値から標準偏差 何個分離れているか、を見るのが基準化変量です。
テスト受けた人全員のそれぞれ点数から平均値を引いて、すべてを足し合わせると0になります。つまりテストの点数の偏差の中心は0になります。基準化変換とは、
- 平均点を0
- 標準偏差を1
としたときの正規分布で、自分の点数を考えることになります。
平均点を0、標準偏差を1 としたときの正規分布を標準正規分布といいます。
参考記事 基準化の意味と基準化変量の求め方(標準化ともいう)
また、そもそも正規分布とは?なんなのかは、次の記事を参考にしてください。
テストの結果を基準化変換し、平均点を0点として、標準偏差を1とすることで、複数のテストの結果を比較できるようになります。今回行われたテストの平均点と標準偏差は、
- 平均点 64点
- 標準偏差 8点
であったとします。
自分の点数が80点であれば、自分の点数から平均点を引いた数値、つまり偏差は16です。平均点よりも16点大きな点数をとっていることになります。この偏差が標準偏差 何個分離れているのか、つまり基準化変量の値はいくつなのかを見ます。
計算すると下記のようになります。
$$(80-64)\div8=2$$
基準化変量は2です。自分の点数80点は、標準偏差2個分プラス側に離れていることになります。
標準正規分布のなかで自分の位置を確認する
平均値は0、標準偏差を1にした標準正規分布で、自分の点数の標準偏差は2ということがわかりました。
基準化変換は偏差を標準偏差で割るわけですから、自分の点数が平均値とまったく同じであった場合、基準化変量は0となります。
$$(64-64)\div8=0$$
- 平均値と同じ点数をとったのであれば、数値は0
- 標準偏差1個分大きい得点であれば基準化変量は1
- 逆に標準偏差1個分小さい得点であれば基準化変量は-1
といった具合です。
この基準化変量の数値がいくつになるのかを見ていきます。テストの点数は正規分布すると考えると、受験生のそれぞれの点数は、
- 68.26%の確率で、標準偏差±1の範囲に、
- 95.44%の確率で、標準偏差±2の範囲に、
おさまることがわかっています。これは、この場合であれば、
- 68.26%の確率で、基準化変量±1の範囲に、
- 95.44%の確率で、基準化変量±2の範囲に、
おさまることがわかっています。と置き換えてもいいです。
このように、偏差値を計算する過程で、平均点と標準偏差が関わっています。
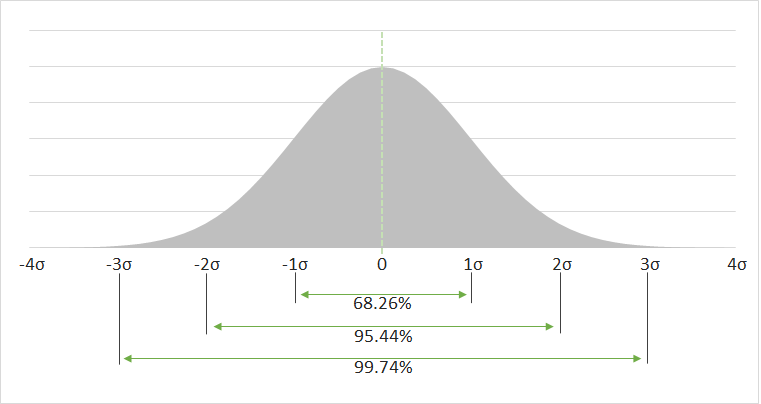
正規分布とはこのような左右対称の分布です。
偏差値は、95.44%の確率で、基準化変量±2の範囲におさまるわけですから、基準化変量が+2を越える、または-2未満になるのは、4.56%以下の確率でだいぶ少ないわけです。
+2を越えるになる確率は、2.28%しかないです。
平均値64点・標準偏差8点のテストで、80点をとったということは、基準化変量は+2になりますから、全体の上位2.28%の実力者ということになりますね。
逆に、平均値64点・標準偏差8点のテストで、48点をとったとすると、基準化変量は-2になりますから、全体の下位2.28%に位置することになります。
基準化変量をみることで、自分の点数がテストを受けた人たちの中で、どのくらいに位置しているのか把握したり、複数の異なるテストの結果を比較することができるようになります。
基準変化量から偏差値へ
基準化変量は、0を中心として、マイナスの値も出てくることになりますし、だいたいの数値が、-3~+3の間に収まり、数値はたとえば0.6とか1.3というように小数点を含んだ小さな数値になります。
このままでも、相対的な自分のレベルはわかるのですが、もっと得点らしい数値にするために、数字を大きくしたものが偏差値です。
平均値0、標準偏差1の分布で基準化変量を見るのではなく、平均値を50、標準偏差を10と設定した分布の中での見る値が偏差値です。
そこで出てくるのが、最初に紹介したこちらの式です。
\(50+\frac{自分の点数-平均点}{標準偏差}\times10\)
上記した
- 平均値 64点
- 標準偏差 8点
のテストで80点をとった場合の偏差値の計算の仕方です。まず基準化変量を求めます。
$$基準化変量=(80-64)\div8=2$$
標準偏差2個分、平均値よりも高い点数をとっています。
基準化した状態では標準偏差は1なので、標準偏差を10にして考えるには、基準化変量も10倍にすればよいです。平均値は50として、ここから20離れているわけです。
$$50+(2\times10)=70$$
偏差値は70となりました。
偏差値で相対的な自分のレベルを確認する
正規分布では、受験生のそれぞれの点数は
- 68.26%の確率で、平均値±標準偏差1個分の範囲に、
- 95.44%の確率で、平均値±標準偏差2個分の範囲に、
におさまります。よって、
- 68.26%の確率で、偏差値50±10の範囲に、
- 95.44%の確率で、偏差値50±20の範囲に、
受験生の点数がおさまると考えますから、偏差値30~偏差値70の間に95.44%という大多数の受験生が含まれます。
偏差値30未満、偏差値70を越える受験生は、合わせて4.56%になります。
偏差値30未満の人だけは半分の2.28%、偏差値70を越える人も同じく2.28%となりますね。偏差値70を越える人は、かなりよい成績であることがわかります。
偏差値70前後が必要になる日本国内トップクラスの大学に入れるような人は、受験生のなかで上位2.28%にくい込むことができる、相当な実力者であることがわかります。