基準化の意味と基準化変量の求め方（標準化ともいう）

正規分布は平均値と標準偏差で決まると書きました。 正規分布に含まれるデータｘがある値以下になる確率、データｘ₁からｘ₂までの確率など、データがある範囲に入る確率を算出することができます。

参考記事　正規分布の形など特徴や性質

そのためには、データｘの偏差を標準偏差1単位あたりの偏差に変換をします。この値のことを基準化変量といいます。この記事で基準化変量について書きました。

基準化変量を求める

データｘの偏差を標準偏差1単位あたりの偏差に変換することを「基準化変換」といい、この標準偏差1単位あたりの偏差を「基準化変量」といいます。言い換えると、あるデータの偏差が、平均値から標準偏差が何個分で離れているかを見るものです。「標準化」ともいいます。

基準化変量はｚで表します。

• 平均点を0
• 標準偏差を1

としたときの分布を考えることになります。基準化変換するのは0点として、偏差が標準偏差何個分が離れているのかをみればいいので、データｘの偏差を標準偏差で割れば、基準化変量ｚを算出できます。

成人女性の身長の分布で考えてみましょう。平均は160cmと標準偏差は5cmとします。

身長165cmの人であれば、平均身長160cmを引いた数値、つまり偏差は5です。平均点よりも5cm大きな身長になります。

基準化変量を計算すると下記のようになります。

偏差 ÷ 標準偏差

＝（165－160）÷ 5

＝1

基準化変量は1です。165cmの人は、標準偏差1個分プラス側に離れていることになります。平均値は0、標準偏差を1にした分布で、標準偏差は1ということです。

基準化変換は偏差を標準偏差で割るわけですから、身長が平均値とまったく同じであった場合、基準化変量は0となります。

160cmの人であれば、
（160－160）÷5
＝0

また、

170cmの人であれば、
（170－160）÷5
＝2

150cmの人であれば、
（150－160）÷5
＝－2

これが基準化変量ｚになります。

基準化変量から確率を計算する

データを基準化変量ｚに変換し、ｚ値を統計数値表に照らし合わせると、そのｚ値以下をとる確率や、そのZ値以上をとる確率などが計算できます。

統計数値表は、統計学で行われる計算作業を省略するため、統計学に関する様々な数値をあらかじめ計算して表にまとめたものです。 基準化変量ｚの値がいくつになったら、確率は○○以下、と計算された表があります。

ｚ値から確率を計算するための表は、標準正規分布表といい、統計学の書籍の巻末には必ずつけられているはずです。

下記は、標準正規分布表は細かく記載されていますから、そこから一部分だけを抜き取った表です。

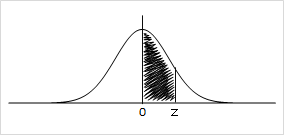
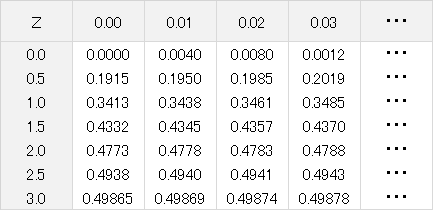
縦に見て一番左の列は、ｚ値の整数小数第1位までを示し、 横に見ていちばん上の行の0.00、0.01、0.02・・・の数字は、小数第2位を示しています。ｚ値が1.52であれば、一番左の列で1.5を探し、そこから右へ3つ進むとｚ値1.52の欄です。

ここに書かれている数値は0.4357ですね。これが表の上に書かれているグラフの0からｚ値までの黒塗りされた箇所の面積です。つまり、分布全体の中の割合を示しており、ランダムにデータを抜き取ったとしたら、43.57%の確率で平均値0からZ値1.52の範囲内の値になるということです。

成人女性の身長は平均は160cmと標準偏差は5cmで、基準化変量ｚは、

170cmの人であれば、
（170－160）÷5
＝2

160cmの人であれば、
（160－160）÷5
＝0

150cmの人であれば、
（150－160）÷5
＝－2

でした。

170cmの人であれば、ｚ値は2ですから、正規分布表のｚ値の列を見て、2.0を見つけます。 少数第2位は0ですから、ひとつだけ右の欄に進んで、0.00の列にある数値をみます。0.4773ですから、平均身長160cmから170cmの範囲の割合は、47.73％となります。

また、170cm以上の人の割合を計算することもできます。分布グラフ中央から右半分は50％ですから、そこから160～170cmの範囲である47.73％を引けばよいのです。

50.00 － 47.73 ＝ 2.27%

と計算できます。ｚ値以上の人、つまり170cm以上の人は、全体の2.27％であることがわかります。