相関分析とは、2個の変量の関係がどれだけあるのかを判断する分析です。
- 一方の変量が増加すると、もう一方の変量も増加する
- 一方の変量が増加すると、もう一方の変量は減少する
- 一方の変量が減少すると、もう一方の変量も減少する
- 一方の変量が減少すると、もう一方の変量は増加する
データやグラフを見るだけでも傾向はわかるかもしれませんが、どれだけの相関関係があるのか、はっきりとした数値が欲しいものです。
そんなときに相関係数が役立ちます。相関係数とは、数値で表すことができる指標です。相関係数によって、2つのものごとの関係性を数字で把握することができます。
相関関係の数値化は、扱うデータが量的データなのか、質的データなのかによって、またはどういった尺度なのかによって、計算する方法が変わります。
- 間隔尺度と間隔尺度の場合は、ピアソンの積率相関係数
- 間隔尺度と名義尺度の場合は、相関比
- 名義尺度と名義尺度の場合は、クラメールの連関係数
- 順位尺度と順位尺度の場合は、スピアマンの順位相関係数
の4種類があります。この記事では、この4種類の相関関係の数値化方法について解説します。
量的データ・質的データまた尺度について
相関関係の数値化方法の前に、データの分類について、まとめておきます。
データの分類すると、数字で測ることができるかどうかで、質的データと量的データに分けることができます。
- 質的データは、数字で測ることができないデータ
- 量的データは、身長とかモノの値段のように、数字で測ることができるデータ
となっています。
データの尺度としては、
- 単に名称として使われている名義尺度
- 数字の順位や順番のみが意味を持つ順位尺度
- 数値の間隔に意味がある間隔尺度
- 間隔に加えて比率にも意味がある比率尺度
があります。
質的・量的の分類と、尺度を合わせて考えると、
質的データは、名義尺度と順序尺度
量的データは、間隔尺度と比率尺度
となります。
相関関係の数値化をするときには、扱うデータがどこに属しているかで、やり方が変わります。
量的データと質的データ、尺度についてはこちらの記事を参考にしてください。
それでは、データの種類ごとに相関関係の数値化方法を解説していきます。
量的データと量的データの場合は、ピアソンの積率相関係数
量的データ(間隔尺度、比率尺度)同士の場合は、ピアソンの積率相関係数で相関関係を数値化します。
相関係数 = xとyの共分散 / (xの標準偏差 × yの標準偏差)
- xが増えると、yも増えるという関係を、正の相関関係
- xが増えると、yは減るという逆に動く関係を、負の相関関係
といいます。
相関係数は、-1 ~ 0 ~ 1 の間の値となります。
正の相関関係が強いほど、相関係数は1 に近づき、負の相関係数が強いほど、相関係数は1 に近づきます。
参考記事 相関関係の意味と相関係数の計算方法
量的データと名義尺度(質的データ)の場合は相関比
量的データ(間隔尺度、比率尺度)と名義尺度(質的データ)の場合は、相関比で相関関係を数値化します。相関比は、グループ内のバラつきと、グループ間のバラつきを見るものです。
旅行先の候補として、北海道、軽井沢、ハワイがあったとしましょう。年齢によって、好む行き先が違うのかどうか、アンケートをとってみました。
| № | 年齢(才) | 行きたい場所 |
|---|---|---|
| 1 | 28 | ハワイ |
| 2 | 24 | ハワイ |
| 3 | 29 | 北海道 |
| 4 | 35 | 北海道 |
| 5 | 42 | 北海道 |
| 6 | 45 | 軽井沢 |
| 7 | 55 | 軽井沢 |
| 8 | 47 | 軽井沢 |
| 9 | 37 | 北海道 |
| 10 | 32 | ハワイ |
| 11 | 31 | 北海道 |
| 12 | 51 | 軽井沢 |
| 13 | 49 | 軽井沢 |
| 14 | 30 | ハワイ |
| 15 | 29 | ハワイ |
行き先事に年齢データをまとめると、
| 北海道 | 29、35、42、37、31 |
| 軽井沢 | 45、55、47、49、51 |
| ハワイ | 28、24、32、30、29 |
となりました。
北海道を選んだ人たちの年齢、軽井沢を選んだ人たちの年齢、ハワイを選んだ人たちの年齢に違いがあるのかどうかを調べます。
グラフをつくって見てみましょう。
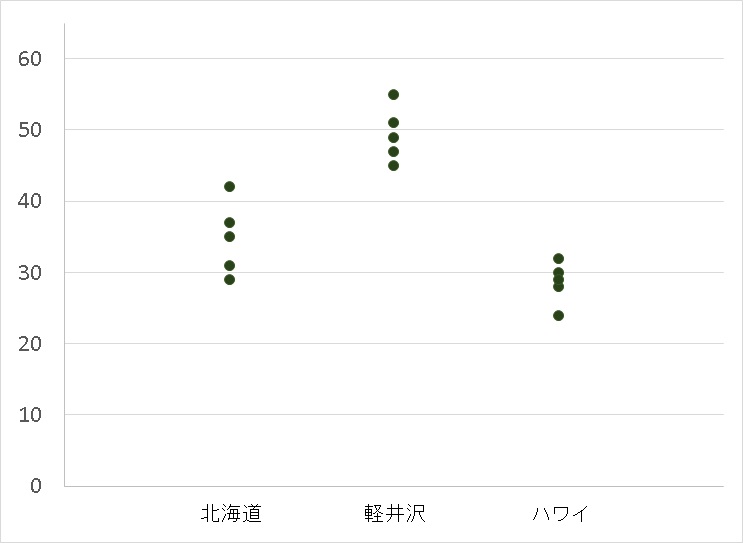
北海道を旅行先として好む年代、軽井沢を旅行先として好む年代、ハワイを旅行先としてこのむ年代には、違いがあるように見えますね。
- 北海道は30代~40代前半
- 軽井沢は40代から50代
- ハワイは20代~30代前半
から好まれるようですね。
これを数値で捉えるために、相関比があります。
北海道のグループ、軽井沢のグループ、ハワイのグループ、グループの間での変動が、全体の変動と比較して大きければ、それぞれのグループに違いがあると言えそです。
グループ内の変動を級間変動、グループ間の変動を級間変動といいます。
相関比 = 級間変動 / 全変動
で相関比計算することができます。
名義尺度(質的データ)と名義尺度(質的データ)の場合は、クラメールの連関係数
名義尺度(質的データ)と名義尺度(質的データ)の場合は、クラメールの連関係数で相関関係を数値化します。
名義尺度と名義尺度のデータである場合は、クラメールの連関係数をつかって関係性を数値化します。
軽井沢は行きたいと思うか?と各年代にアンケートをとってみました。
| 20代 | 30代 | 40代 | 50代 | 合計 | |
|---|---|---|---|---|---|
| 行きたい | 2 | 2 | 5 | 7 | 16 |
| 行きたくない | 6 | 6 | 1 | 0 | 13 |
| 合計 | 8 | 8 | 6 | 7 | 29 |
回答者には、回答者の年代と行きたいかどうかを答えてもらいました。これらの2つの質的データを行と列の項目として、かけあわせたところに記入をします。
たとえば、30代で、軽井沢に行きたくない人は、8人いたということです。
クロス集計表のデータ数をn、行列の短い方をkとすると、次の式でクラメールの連関係数を計算できます。(この表の場合はn=29、k=2)
クラメールの連関係数 = \(\sqrt{\frac{\chi^2}{n(k-1)}}\)
順位尺度(質的データ)と順位尺度(質的データ)の場合は、スピアマンの順位相関係数
順位尺度(質的データ)と順位尺度(質的データ)の場合は、スピアマンの順位相関係数で相関関係を数値化します。
行きたい旅行先を順位をつけて選んでください。と2人の回答を得ました。
| 北海道 | 軽井沢 | ハワイ | 中国 | |
|---|---|---|---|---|
| Aさん | 2 | 1 | 3 | 4 |
| Bさん | 4 | 3 | 2 | 1 |
AさんとBさんの好みに相関があるのかどうか調べる、スピアマンの順位相関係数です。
2人のつけた順位の差の2乗を計算します。
| 北海道 | 軽井沢 | ハワイ | 中国 | |
|---|---|---|---|---|
| Aさん | 2 | 1 | 3 | 4 |
| Bさん | 4 | 3 | 2 | 1 |
| 順位の差 | -2 | -2 | 1 | 3 |
| (順位の差)2 | 4 | 4 | 1 | 9 |
1位から4位までの順位を与えました。順位の数をnとして、次の式でスピアマンの順位相関係数を計算できます。
Σ(順位の差)2 / n(n2-1)
まとめ
2つのものごとの相関関係を求めるには、データの種類に着目して、それに合った相関の数値化方法を選びます。
- 量的データ(間隔尺度、比率尺度)同士の場合は、ピアソンの積率相関係数
- 量的データ(間隔尺度、比率尺度)と名義尺度の場合は、相関比
- 名義尺度と名義尺度の場合は、クラメールの連関係数
- 順位尺度と順位尺度の場合は、スピアマンの順位相関係数
となります。