幾何平均とは、各平均のデータの値を掛け合わせて、データ個数n乗根をとったものです。
伸び率の平均を計算するときに用いられます。
参考記事 幾何平均(相乗平均)の意味と計算方法~伸び率の平均を求める~
売上が下記のように伸びている会社があるとしましょう。起業して6年、売り上げを伸ばし続けている会社です。
- 1年目の売上 2000万円
- 2年目の売上 2500万円 125%
- 3年目の売上 4000万円 160%
- 4年目の売上 8000万円 200%
- 5年目の売上 1億2000万円 150%
- 6年目の売上 1億5000万円 125%
初年度からの5年間、伸び率の年平均の計算したいとしましょう。その場合、求めるのは幾何平均です。計算方法は、
「各年度の伸び率データを掛け合わせて、データ個数の五乗根をとる」
です。
$$\sqrt[5]{1.25\times1.6\times2.0\times1.5\times1.25}\\=1.49628…$$
売上伸び率の年平均は、1.49628 (149.628%)となりました。
この幾何平均の計算は、エクセルの関数で行うことができます。
エクセルのGEOMEAN 関数で計算する
幾何平均はエクセルのGEOMEAN 関数で計算することができます。
幾何平均のことを英語では、「geometric mean」といいますから、GEOMEAN 関数という名前になっているのでしょう。
表に売上を記入し、合わせて伸び率も記入します。
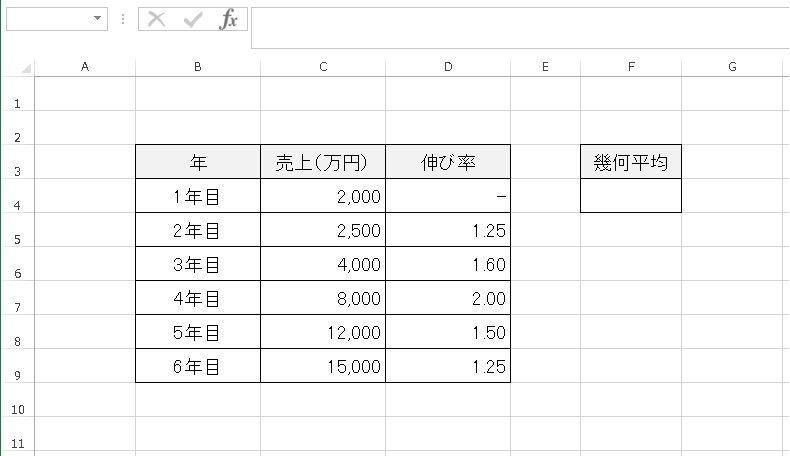
「=GEOMEAN(データ範囲) 」を入力します。
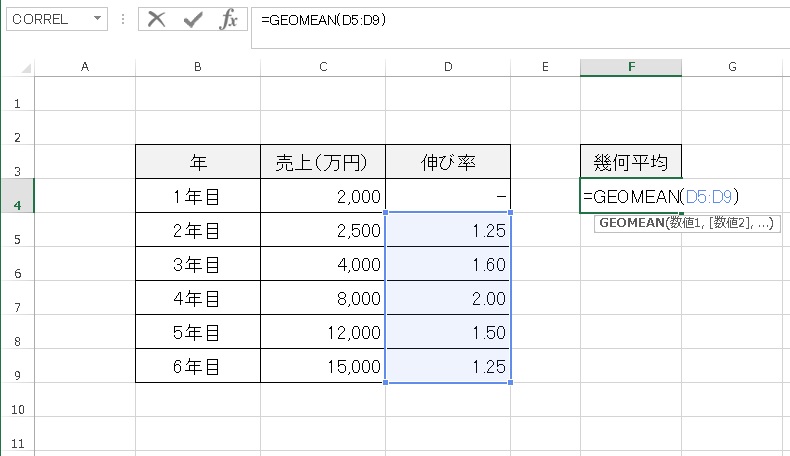
幾何平均の値が表示されます。
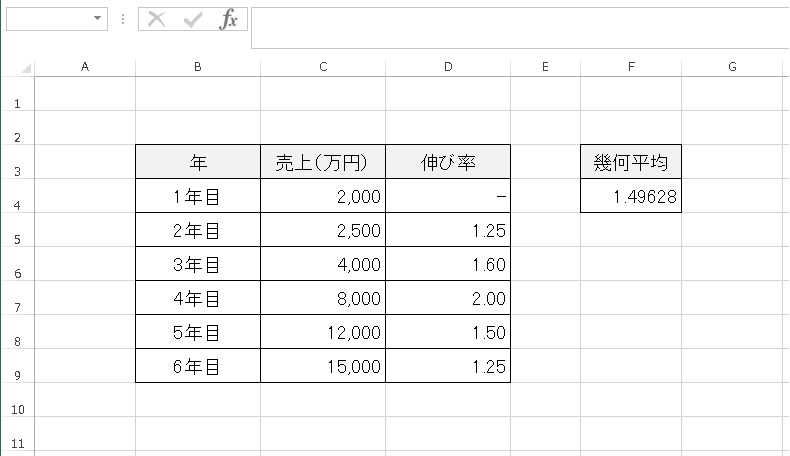
平均すると1年間に売上が1.49628倍になっているわけです。1年目の売上に2000万円に1.49628を5回かけると、
2000万 × 1.496285 = 1億5000万円
となり、6年目の売上と一致します。