製品の品質が求められる規格に対して満足な状態なのか、製品を生み出す工程の実態を把握するための指標が、工程能力指数(Process Capability Index)です。
工程能力指数とは、規定された規格の幅に対して、実際の工程のデータがどの程度ばらついているかを見る指標です。規定された規格の幅を実際の工程ばらつきで割ることで計算できます。
工程能力指数は、記号でCpと表します。
工程能力指数の計算式
製品の規格幅と実際の製品の標準偏差を用いて計算します。
製品の規格幅とは、基準の幅ということです。ここを越えたらNG品という上限の基準と、ここを下回ったらNG品という下限の基準があります。
規格上限値・下限値は、許容限界ともいいます。
中心から両側 に許容限界がある場合
工程能力指数
= 規格幅 / 工程のばらつき
= (規格上限値-規格下限値)/ (6×σ)
で工程能力指数を計算できます。
規格上限値(上の許容限界)をUTL、規格下限値(下の許容限界)をLTLとすると、
$$\frac{UTL-LTL}{6σ}$$
片側に許容限界がある場合
工程能力指数
= (規格上限値-平均値)/ (3×σ)
または (平均値-規格下限値) / (3×σ)
で工程能力指数を計算できます。
許容限界をTLとすると、
$$\frac{|TL-\bar{x}|}{6σ}$$
工程能力の評価
1.00より小さいと工程能力が不足、1.33より大きいと工程能力が充分
工程能力指数によって、下記のように工程能力を評価することができます。
| Cp < 1.00 (1.00より小さい) | 1.00 < Cp < 1.33 (1.00~1.33の間) | 1.33 < Cp (1.33より大きい) |
|---|---|---|
| 工程能力が不足している。 | 工程能力はあるが十分ではない。 品質のばらつきが大きくなると、不良品が発生しやすい。 | 工程能力は十分にある。 |
工程能力指数の値が大きくなるほど、工程能力があるとされます。
再度、計算式を見てみます。
$$\frac{規格上限値-規格下限値}{6×σ}$$
計算式の分子が「製品の規格範囲(基準範囲)」、分母が「6σ」なのですから、分子の「製品の規格範囲(基準範囲)」に対して、分母の工程ばらつき「6σ」が小さいと、工程能力指数の値は大きくなります。
大きい工程能力指数の値は、工程能力があり、優れていることを意味します。
逆に、
分子の「製品の規格範囲(基準)」に対して、分母の工程ばらつき「6σ」が大きいと、工程能力指数の値は小さくなりますよね。
小さい工程能力指数の値は、工程能力がないことを意味します。
工程能力指数が1.00を下回る場合
工程能力指数が1.00を下回る場合は、規格値からはみ出す製品があり、不良品が多く、工程能力は不十分です。常に不良が発生する状態になってしまっています。ばらつきを小さくするための改善を行う必要があります。
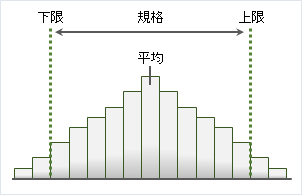
工程能力指数が極端に大きい場合
工程能力指数が1.67 を越えると、十分すぎる工程能力があるとされています。
工程能力指数が小さいと問題ですが、逆に、工程能力指数が極端に大きいと、規格の範囲が広く、ばらつきも小さく、余裕がありすぎることを意味します。
過剰品質になり、工程の管理コストがかかりすぎているかもしれないので、もう少しばらつきがでてもいいので、コスト低減ができないか検討するといいです。
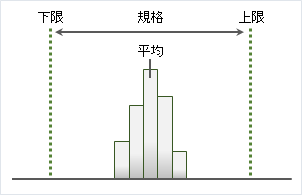
規格値(基準)の中心とデータの平均値を合わせることも大事
工程能力指数も大事ですが、規格値の中心とデータの平均値を合わせることも大事です。
工程能力指数が1.00より大きく規格の幅よりもばらつきが小さいときは、規格の中心とデータ平均値が同じであれば、不良はほとんど見られません。
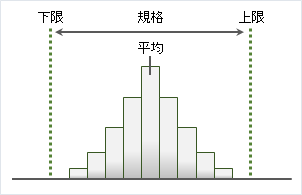
しかし、データ平均値が規格の中心からずれてしまうと、工程能力指数が1.00を上回っていても不良が発生します。データの平均値が規格の中心からずれた場合でも工程能力指数の数値は変わりません。
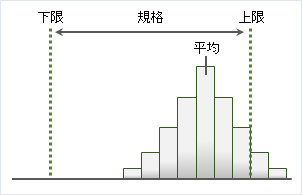
工程能力指数の評価が1.00あっても十分でなく、1.33以上あると十分というのは、上記の図のようにデータの分布の中心が、ズレてしまっても不良品が発生しにくいからです。
規格値の中心と、実際のデータの平均値を合わせることが大事です。ズレている場合は、作業方法の変更や製造機械の調整などで、規格幅の中心とデータの平均を合わせる必要があります。