大数の法則をコイン投げの例でシミュレーションして、わかりやすく考えてみる

大数の法則がどのような法則なのか、日常のできごとやコイン投げを例として解説していきます。

大数の法則とは

大数の法則とは、試行の回数を増やしていくほど、結果は本来の確率に限りなく近づいていくことです。

コインを投げて表が出る回数を数えるとします。

コイン投げの回数を\(n\)、表が出た回数\(r\)とすれば、誤差\(\varepsilon\)がどのように小さい正の数であっても、

$$P(|r/n-0.5|\leq \varepsilon)→1\ \ \ (n→∞)$$

が成り立ちます。

\(r/n\)は実際のコイン投げによって表が出た割合です。それとコイン投げで表が出る理論的確率の差の絶対値が \(|r/n-0.5|\) です。

コイン投げの回数が無限回∞に近づくほど、実現値と理論値の差の絶対値 \(|r/n-0.5|\) は小さくなり、どんな小さい誤差\(\varepsilon\)よりも小さくなります。

「たまたま」は長く続かないもの

ある確率で起こるできごとが繰り返されるとき、それが連続で起こったり、あるいは、逆に連続で起こらなかったりすることはよくあります。

たとえば、相撲という勝負の世界。横綱の力士と格下の力士の勝負。

ふつうは、横綱が勝ちますよね。勝率９割といったところでしょうか。

でも、ある勝負では、横綱力士が不調で、格下力士に連続で負けてしまった。

まあ、たまたま負けが続いてしまうこともあります。が、おそらく、これは長くは続きません。その後の勝負では実力のある横綱がまた負けてしまうことはなく、勝つ可能性が高いでしょう。何戦か続けていけばもともと実力があった横綱の方が勝率は圧倒的に高くなるはずです。

高校のお昼休みに仲間内で昼食のパンを買いに行く人をクジで決めています。ここのところ毎回自分ばかりが負けてパンを買いにいっている気がするなぁと思う…。

たまたまクジで負けが連続することもあります。しかし、10回も20回も連続で負けることはまずないでしょう。

最近サッカーで遊ぶようになった。開始時には最初にボールを持てるチームをコイン投げ決めている。表・裏のどちらがでるかを予想して、当たったほうがボールを持ってスタートできる。

まだやり始めて数回の試合しかしていないけど、毎回コイン投げに勝ってボールをゲットしている。自分はコイン投げに強いから、コイン投げを任されている。

これも、たまたま連続で勝てているだけです。今後、何度も行っていけば、コイン投げに負けて相手がボールを持つことも出てきて、最初にボールをゲットできる割合長い目で見れば1/2に近づいていきます。

偶然○○になった、最近運が悪い…。こういったことは何度も何度も続かないものです。長く続けるにしたがって、しかるべき確率で、結果が出てくるようになるのです。

続ければ続けるほど、横綱は格下の力士より圧倒的に力がありますから何度も戦えば勝ちが多くなって勝率は９割に近づき、自分ばかりがクジに負けて買い出しに行かされることもなくなって仲間内でパンを買いに行く回数は各人で均等に近づき、サッカーの試合前にコイン投げに毎回勝てることはなくなり、勝ってボールを取れるのは確率\(\frac{1}{2}\)に近づいていきます。

このように、何度も何度も回数を重ねることによって、結果は、本来あるべき割合に落ち着いてきます。これは、大数の法則という統計学の理論で説明することができます。

大数の法則をコインを連続で投げてみる

コイン投げの例で考えてみましょう。

ここに500円玉があります。これに強いスピンをかけて上に放り投げ、掌に落とし表が出るか裏が出るか、繰り返して見てみましょう。コイン投げは、コインに細工が無く、よくスピンをかけて投げるのであれば、

• 表が出る確率が\(\frac{1}{2}\)
• 裏が出る確率が\(\frac{1}{2}\)

になるはずです。

まず10回、実際に投げてみました。

表を「H」、裏が出たら「T」と記録しました。

1回目はH、2回目はT、3回目もT、これを続けていくと・・・

表が多く出ました。もう10回行ってみましょう。

今度は5回ずつでちょうど表と裏が$\frac{1}{2}$ずつとなりました。さらに何度も続けて行ってみると、

このような結果になりました。この記事を書いているときに実際に投げていますよ。

連続して同じ面が出るのは、よくあること

意外にも、HとTが順番に出てくることは少ないことがわかります。逆に、HHHHやTTTTと同じ面の出現が連続して見られます。

最後に至っては7回連続でT（裏）が出ていますね。こんなに連続してT（裏）が出るのはおかしいなと思うかもしれません。

また、コイン投げを続けている中で、何度も連続して裏が出続けているときには、「そろそろ次あたりに表が出るかも」と思うかもしれません。

でも、連続でT（裏）が出るのは、実はまったくおかしなことではないのです。それに何度も連続してT（裏）が出たからといっても、次にH（表）が出る確率が高くなることもないです。

それぞれのコイン投げは完全に独立しており、どんな場面であっても次のコイン投げで表が出る確率は\(\frac{1}{2}\)、裏が出る確率も\(\frac{1}{2}\)になります。

あるときのコイン投げの結果は、その後のコイン投げの結果には全く影響を与えません。1回のコイン投げは過去の結果にも未来の結果にもなんら関係がないのです。

何回も連続で表が出続けることもあるし、表・裏・表・裏と交互に出続けることもありえるのです。

回数が少ないと確率は\(\frac{1}{2}\)から離れることがあるが、回数が増えると\(\frac{1}{2}\)に近づいていく

コイン投げを10回単位で区切って結果を見ると、 表（H）が出た割合が１０回中５回で、ちょうど\(\frac{1}{2}\)になっているときもありますが、10回中3回のときもあれば、10回中7回のときもあります。

上の実験では、10回のコイン投げを5回繰り返してみました。各回の表が出た割合です。

• 1回目：\(\frac{4}{10}\)
• 2回目：\(\frac{5}{10}\)
• 3回目：\(\frac{3}{10}\)
• 4回目：\(\frac{7}{10}\)
• 5回目：\(\frac{3}{10}\)

合計すると、\(\frac{22}{50}\)で、表が出た確率は44％でした。

10回だけのコイン投げのときには\(\frac{3}{10}\)や\(\frac{7}{10}\)の結果もあったのに、50回をまとめてみると44％の割合で表が出ており、\(\frac{1}{2}\)の割合に近づいていることがわかります。

コイン投げで表・裏が出る確率は50：50です。

10回くらいの少ない回数で短期的にみると、本来の確率からかけ離れた結果が出ているわけですが、何度もコイン投げを繰り返すことによって、表・裏が出る割合は50：50に近づいていきます。

このように試行の回数を増やしていくほど、結果は本来の確率に限りなく近づいていくことを、大数の法則といいます。

では、コイン投げの回数をさらに重ねてみましょう。自分で投げ続けるのは大変なので、代わりにコンピュータに行ってもらいます。統計ソフトのＲを使って、数字の「1」、「2」がそれぞれ確率\(\frac{1}{2}\)で発生する試行を繰り返しました。「1」を「H（表）」とし、「2」を「T（裏）」と見立ててシミュレーションしました。

コイン投げと言っていますが、コンピュータでの確率\(\frac{1}{2}\)の試行シミュレーションです。あしからず。

※繰り返しになりますが英語で表面をhead、裏面をtailといいますから、その頭文字をとって、表をH、裏をTであらわしています。

最初の10回のコイン投げでは、表の割合は20％ですが、回数を増やすに従って、表の出た割合が50％に近づいているのがわかります。

1千万回行うと、\(\frac{1}{2}\)の割合に限りなく近づいていますね。

しかし、ピッタリと\(\frac{1}{2}\)の確率になるのは、まずありません。確率\(\frac{1}{2}\)というのは、無限回コイン投げを繰り返したときの、理論値なのです。

では、もう一度コイン投げをやってみましょう。次は、続けてコイン投げ続けて各回数のところで、 表が出た割合はどのようになっていくのか推移を見てみます。

まず200回行ってみました。

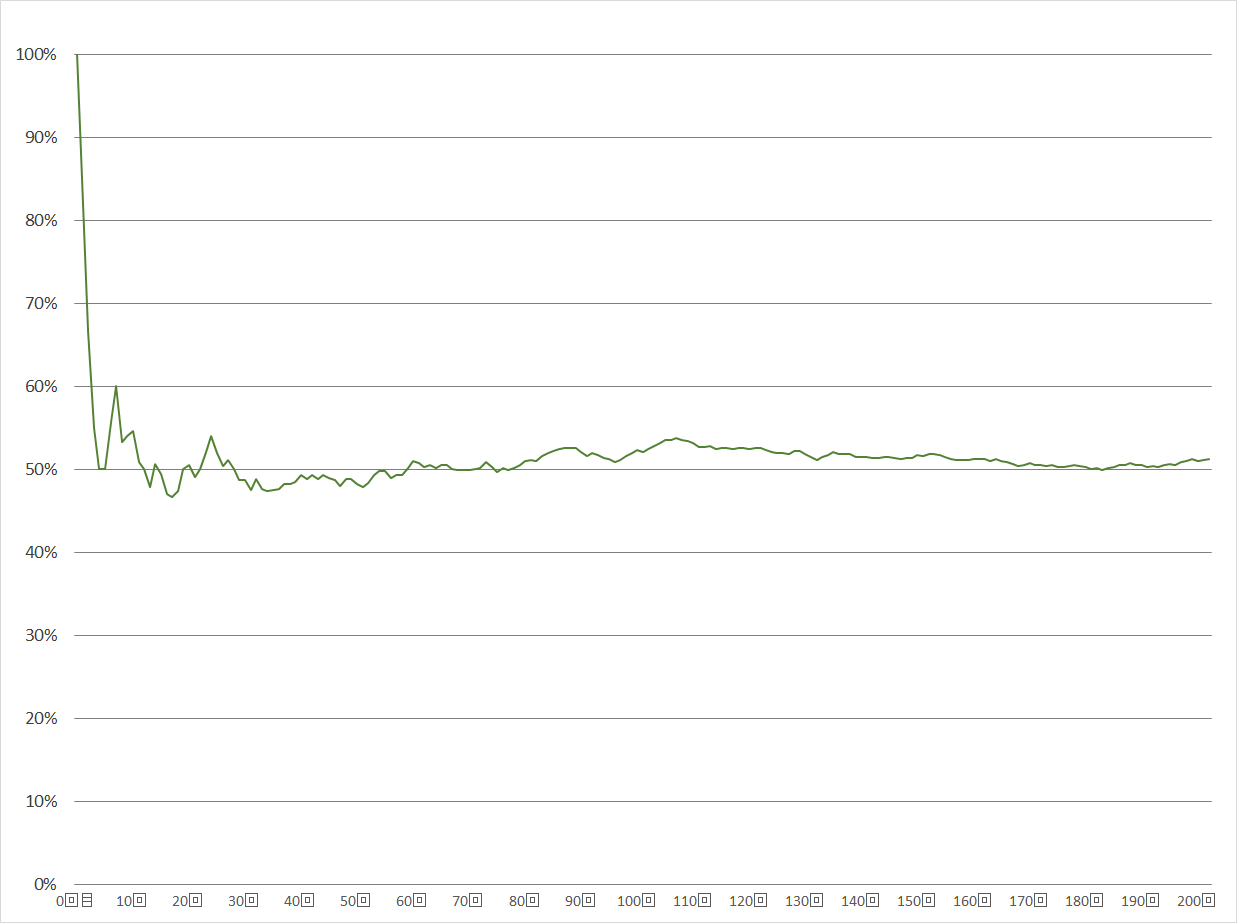
※横軸がコイン投げをした回数、縦軸が全コイン投げのうちで「表」が出た割合%

表が出た割合は最初の数回では60％、その後30～40回目では50％を下回まわり、100回目くらいには、52～53％のところをうろうろしていますが、さらに試行を繰り返して回数を重ねていくことによって、50％に収束していく様子がわかります。

さらに続けて、1000回まで行ってみると、

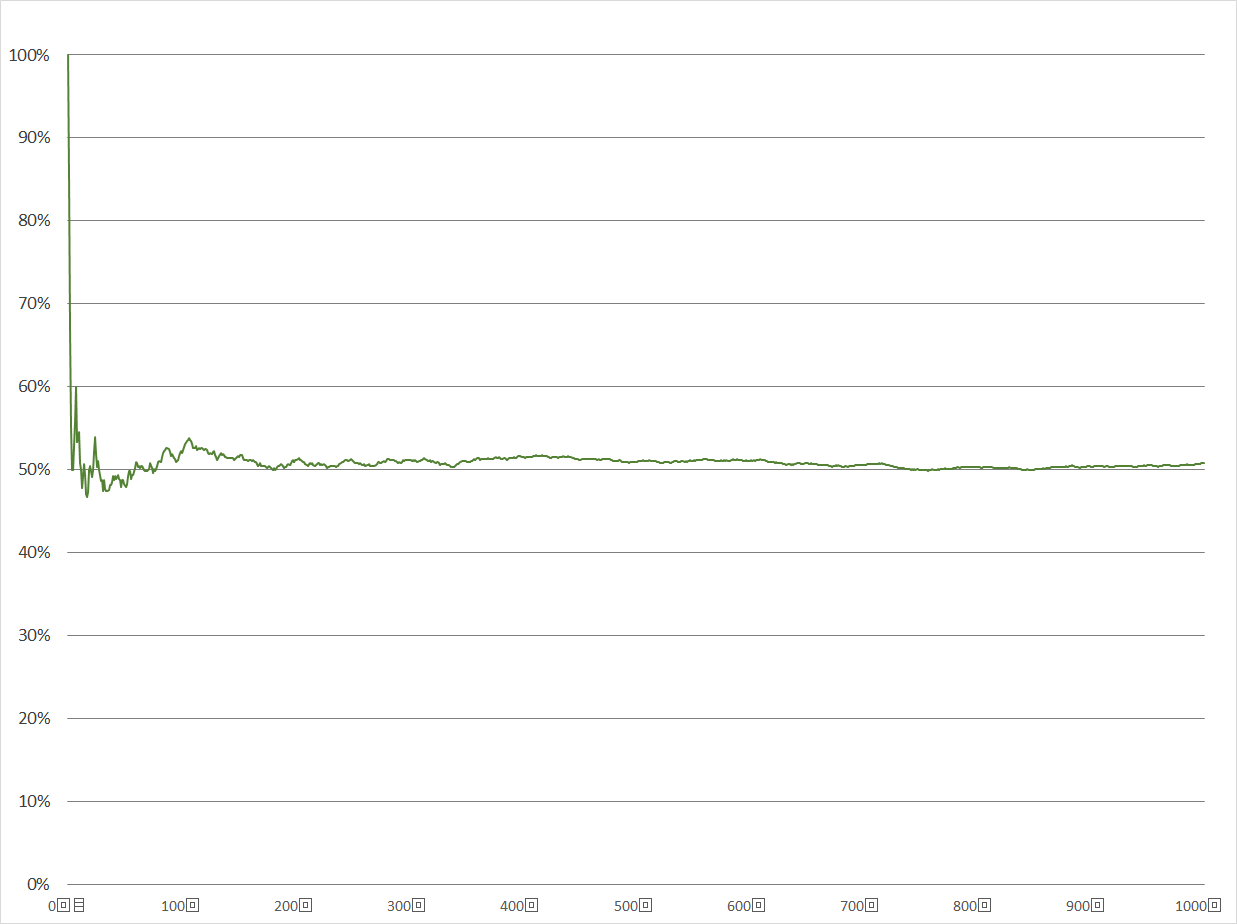
200回でほぼ50％になりましたが、その後は表の出る確率がわずかに高くなり51％くらいを推移し、750回くらいでほぼ50％になり、 その後はずっと50％に収束しています。

たまたま偶然で、本来の確率とは違う結果が出ていても、長く長く試行を続けていると、結果は本来の確率に収束してくる大数の法則の話でした。