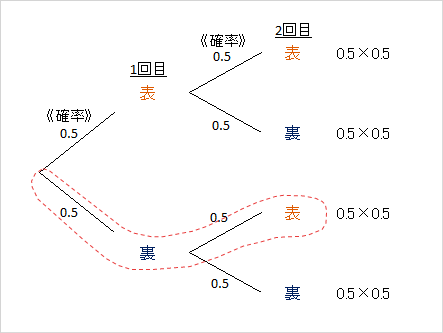
2段階、3段階と確率を計算するとき、有効な図法として「確率の木」があります。 実験の結果起こりうることを網羅し、それらの起こる確率を図にしたものです。
コインを投げ2回連続で行う場合を考えてみましょう。表が出る確率は0.5、裏が出る確率は0.5です。
確率の木を描くと、このようなものになります。
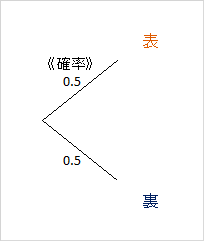
さらに、2回目のコイン投げで起こりうる結果を追加すると、1回目に起こりうる結果、その後2回目に起こりうる結果が続いて描かれます。
コイン投げの結果とその確率が、視覚的に理解しやすいですね。
枝分かれした木のようになるので、確率の木と呼ばれています。
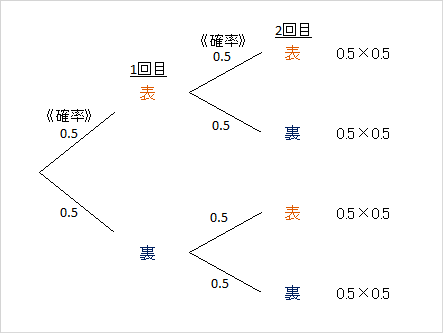
一番右の枝分かれした最後の部分の数が、起こりうる全ての結果の数になり、2回連続でコインを投げるとしたら、全ての結果の数は4です。
1回目に裏が出て、2回目に表がでる確率を見てみましょう。確率の木でそれをたどっていけばいいのです。
1回目は0.5 の確率で裏になります。2回目は0.5 の確率で表、です。それぞれの確率を掛け合わせれば、1回目に裏が出て2回目に表が出る確率を計算できます。
・1回目に裏、2回目に表