分布の形状を見るときに利用されるものとして、歪度があります。この記事では、歪度の意味や求め方について説明します。
歪度とはなにか
「歪度」とは、分布の歪み度合いを示すものです。
正規分布のように左右対称であるのか、それとも片方の裾だけだ伸びたような歪んだ分布なのか、その度合いを示します。
$$歪度=\frac{E[(X-μ)^3]}{\sigma^3}$$
これを歪度(または歪度係数)といって、歪度が0 よりも大きければ右の裾が長い分布、歪度が0 よりも小さければ左の裾が長い分布となります。
通常$z$値を計算(平均が0、標準偏差が1 の標準化)をするときには、
$$\frac{X-μ}{\sigma}$$
で計算しますよね。これを3乗した値の平均が、歪度の値となります。
歪度の数値と分布の形
歪度が0より大きい場合の分布、歪度が0の分布、歪度が0より小さい場合の分布について見ていきましょう。
歪度 > 0
歪度係数が0より大きい場合は、右の裾が長い分布です。
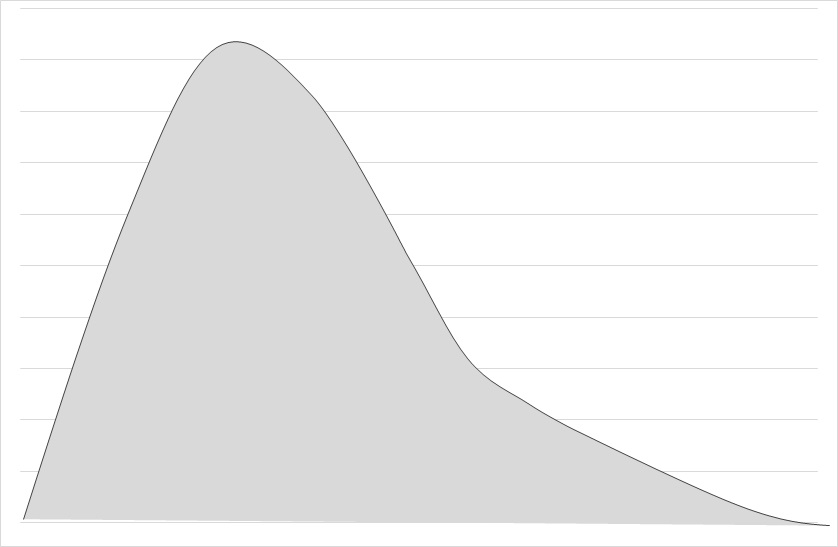
歪度 = 0
歪度が0の場合は、分布の形が左右対称。正規分布のときに0になります。
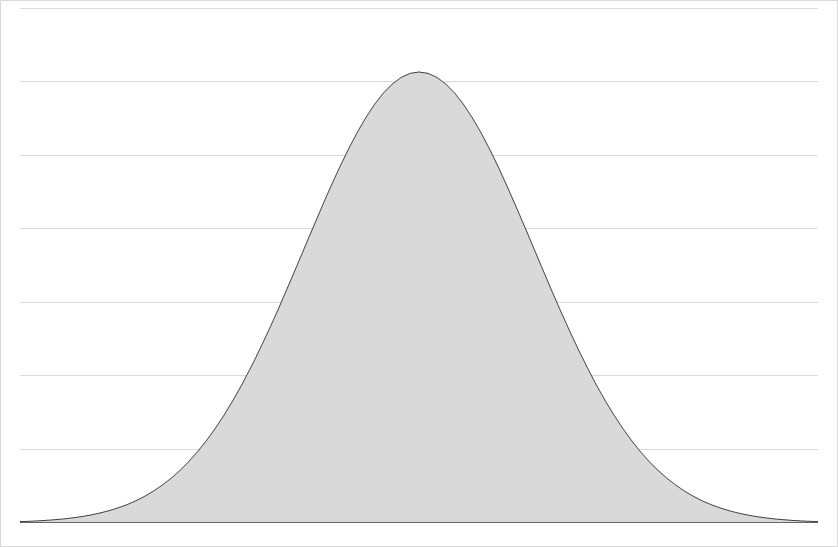
歪度 < 0
歪度係数が0より小さい場合は、左の裾が長い分布です。

ただ、歪度 = 0であったとしても、分布が必ずしも左右対称であるということではなく、標準化した\(z\) 値の平均値(=0)の右側にある\(z^3\)の和と、左側にある\(z^3\)の和が一致しているということです。
歪度の絶対値が小さければ、標準化した\(z\) 値の平均値(=0)の右側にある\(z^3\)の和と、左側にある\(z^3\)の和の差が、小さいことになります。
なぜ3乗で計算し、歪度が0を越えると右の裾が長い分布を示すことになるのか
歪度は、なぜこのように3乗して計算し、0を越えると右の裾が長い分布、0より小さいと左の裾が長い分布を示すことなるのでしょうか。
まず、歪度がプラスの値なのかマイナスの値なのかは、もともとの\(z\) 値(=\(\frac{X-μ}{\sigma}\))によります。
\(\frac{X-μ}{\sigma}\)の値がプラスの値であれば、3乗をしてもプラスの値です。しかし\(\frac{X-μ}{\sigma}\)の値がマイナスであれば、2乗であれば、マイナスが消えてプラスの値となりますが、3乗をすると、またマイナスの値となります。
右の裾が長い分布だと、\(z\) 値(=\(\frac{X-μ}{\sigma}\))の平均から遠く離れたデータが右の裾の先にあります。
歪度の計算では、それらの値を3乗します。
$$\frac{1}{n}\ \sum(\frac{X_i -μ}{\sigma})^3$$
すると大きな値となりますから、他の結果として歪度の値もプラス方面に大きくなりやすいのです。
逆に左の裾が長い分だと、左の裾の先に平均から離れたマイナスのデータがありますから、結果として歪度の値がマイナス方面に数値が出ます。
データの値が平均値から絶対値1を越えて、平均値から離れるほど、3乗した値は大きくなります。
ですから、右の裾が長い分布であるほど、歪度も大きな値となるのです。
引き続き、右裾の長い分布の図を見ながら考えてみましょう。

長く伸びた右裾の部分にあるデータから計算した、\((\frac{X-μ}{\sigma})^3\)の値は3乗される効果によって大きくなりますよね。逆に左裾は長くないのですから、\((\frac{X-μ}{\sigma})^3\)の値も、あまり大きくならないでしょう。
それらの値を平均すると、右裾が長ければ長いほど、大きなプラスの値になるはずです。
■歪度係数と分布の形の関係
- 歪度>0(歪度が0より大きい)・・・右の裾が長い分布
- 歪度=0・・・左右対称の分布、中心から左の\(z^3\) の和、右の\(z^3\) の和が一致
- 歪度<0(歪度が0より小さい)・・・左の裾が長い分布
■非対称性の程度
- 歪度の絶対値の大きさで、非対称性の程度を示すことができる
- 片側の裾が長く伸びた分布など、片側だけに平均から離れているデータが多いと、歪度の絶対値は大きくなる
歪んだ分布の例(どんなグラフが、どんな歪度係数になるか)
次のグラフは、右裾が長い分布です。この歪度を、エクセル関数SKEWで調べると、0.795でした。
■歪度=0.795
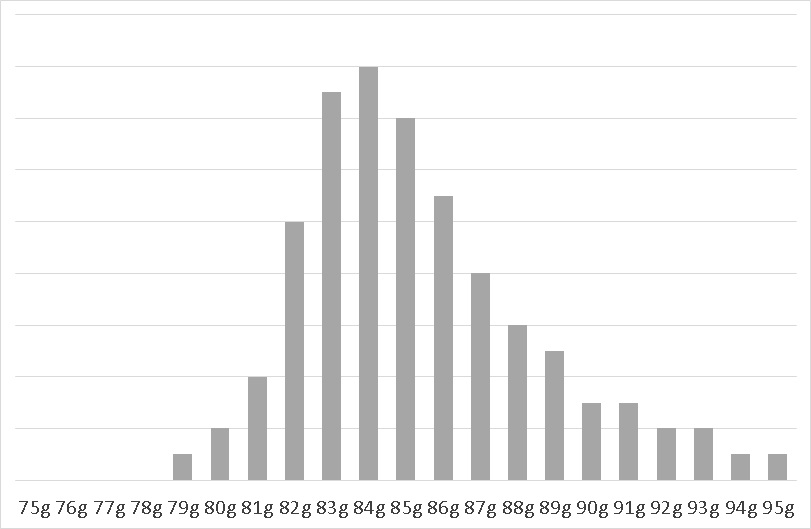
次は、正規分布に近い分布です。この歪度を、エクセル関数SKEWで調べると、0.035でした。
■歪度=0.035
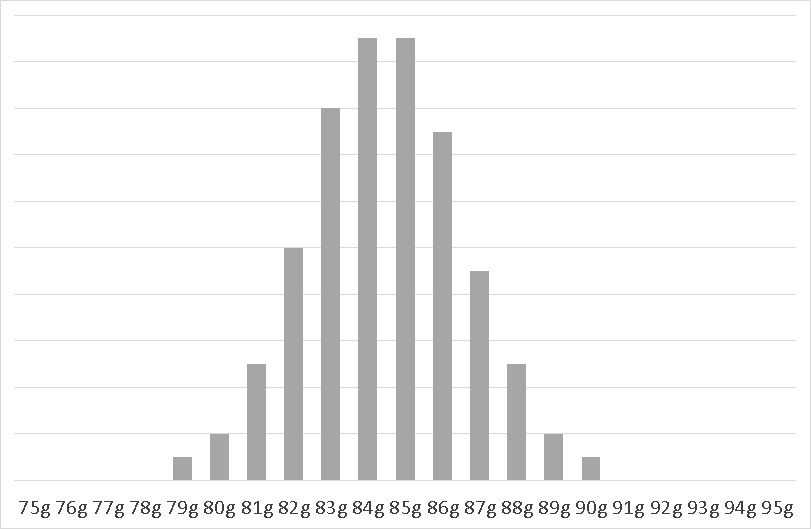
正規分布のように左右対称であれば、歪度=0 となり、このグラフのように左右対称に近ければ、歪度も0 付近になります。
とはいえ、歪度が0 または0 に近いことは、分布が必ずしも左右対称であるということではなく、標準化した$z$値の平均値(=0)の右側にある$z^3$の和と、左側にある$z^3$の和が一致しているということです。
たとえば、ひとつ上に掲載した右裾の長い分布は、歪度 0.795 でした。ここに75g、76gのデータを少し加えてみると、歪度係数は 0.075 となり、0 に近くなってしまいました。
■歪度 = 0.074
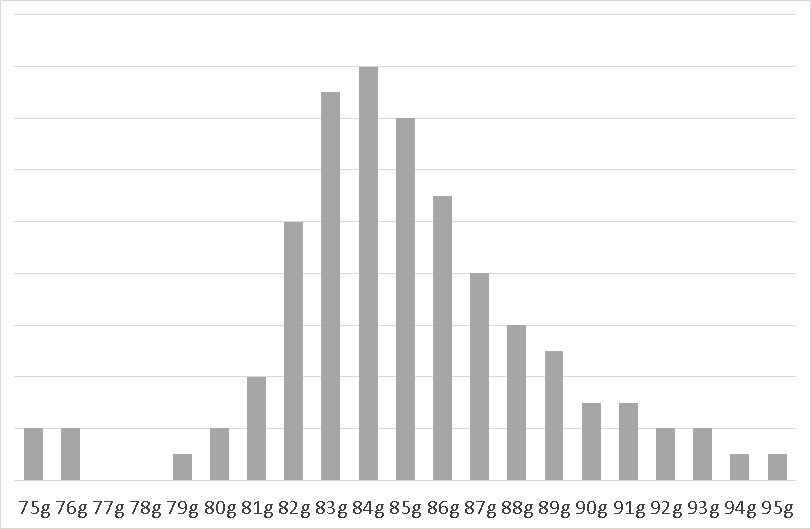
歪度が0に近いですが、左右対称という感じではありません。
次は、歪度=0.795 の右裾が伸びた分布に、77gのデータをいくつか加えてみたものです。歪度係数はマイナスに傾きました。
■歪度= -0.595
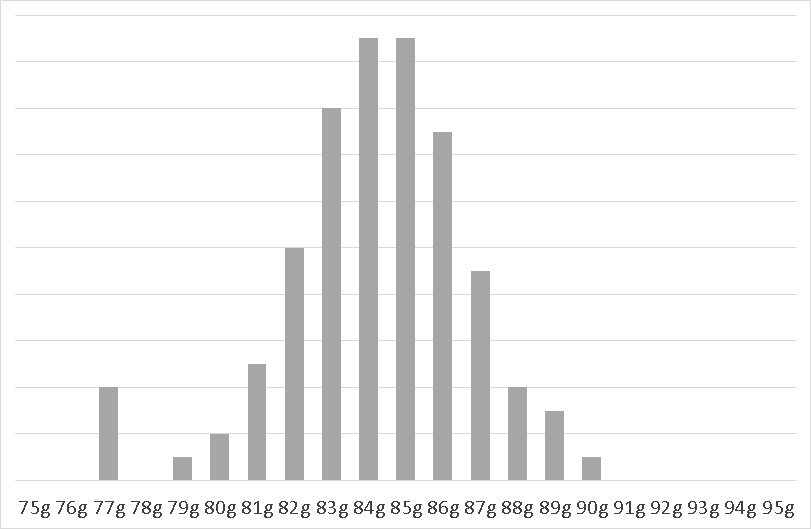
片側の裾が伸びているわけではなく、大きく外れた値の影響であっても、歪度係数は変わってしまうようですね。