歪度とは
分布が左右対称であるかどうかを示すものが、歪度（または歪度係数）です。
歪度は、
$$歪度=\frac{E[(X-μ)^3]}{\sigma^3}$$
で計算することができます。\(\frac{X-μ}{\sigma}\)を3乗した値の平均値です。
値が0 より大きいと右の裾が長い分布、0 より小さいと左の裾が長い分布となります。そして、歪度の絶対値が大きいほど、非対称性の程度が大きいことを示しています。
エクセルSKEW 関数での歪度の計算方法
歪度は、エクセルのSKEW関数で求めることができます。
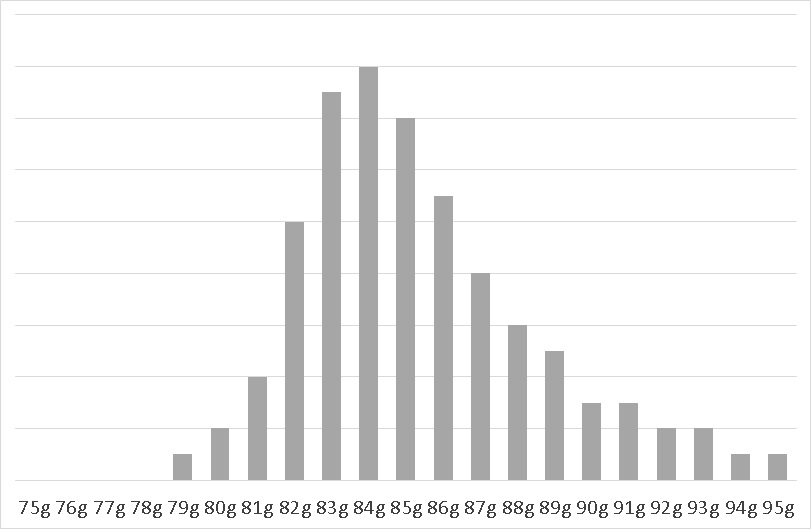
とある工場で製品の重量データをとってみると、次のようなデータが得られたとしましょう。
85、89、87、86、87、85、84、86、89、87、89、86、81、80、88、87、89、84、85、84、92、92、93、87、94、84、91、85、85、85、85、84、86、83、87、89、88、84、83、86、83、84、84、85、84、82、90、90、91、85、83、81、79、82、91、85、95、84、82、83、83、84、85、81、82、82、83、86、84、83、80、82、83、88、83、85、86、83、85、86、83、82、83、88、88、84、82、87、88、86、82、83、93、90、87、84、83、82、84、86、84、86、81、85
グラフにすると、右に長く尾をひいた分布となりました。
エクセルで計算するには、セルに
「＝SKEW（ ）」
を入力し、
「＝SKEW（データ範囲）」
データ範囲を指定してあげると、歪度が表示されます。
このデータを計算してみると歪度は、0.795になりました。
たしかに、右裾の長い分布で、歪度が0よりも大きくなっていますね。（ 歪度 ＞ 0 ）
SKEW 関数とSKEW.P 関数
歪度を計算する関数には、SKEW 関数とSKEW.P 関数があります。
エクセルのヘルプを見ると、SKEW 関数の計算式は、
$$\frac{n}{(n-1)(n-2)}\sum(\frac{X_i -\bar{x}}{s})^3$$
と掲載されています。
一方、SKEW.P 関数で計算した結果は、
$$\frac{E[(X-μ)^3]}{\sigma^3}$$
$$\frac{1}{n}\ \sum(\frac{X_i -μ}{\sigma})^3$$
の式の計算結果と同じになるようですね。