ヒストグラムの見方。その形から背景を読む

ヒストグラムの形をみることによって、その母集団や、データを得られた背景のにある情報を把握することができます。

モノづくりにおいて、製品の規格値を測定したデータのヒストグラムの形を見ることで、工程が正常であったのか・それともなにか問題があったのかといったことを読みとることができます。

この記事では、

• ヒストグラムからわかること
• それぞれのヒストグラムの形に、どんな特徴や意味があるか

を説明します。

左右対称型

中中心あるいは中心前後の度数がもっとも多く、左右対称に近い形です。正規分布としてとらえることができます。

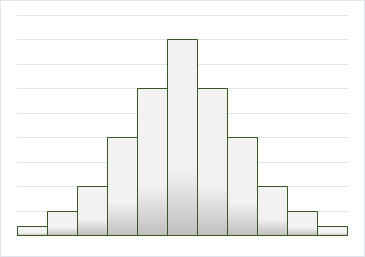
製品の規格値であれば、通常平均値を山の頂点として、そこから左右にばらつきがみられます。

平均値を中心とした左右対称型のヒストグラムが見られるときには、ばらつき度合いが問題ないのであれば、工程は安定していると考えられます。

離れ小島型

ヒストグラムの山から一部のデータが離れたところにあります。

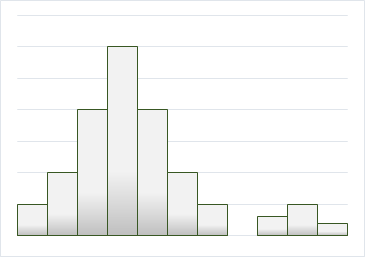
離れたデータが1つや2つであれば、 突発的にできてしまった製品であったり、測定に間違いがあった可能性があります。

モノづくりをする工場で得られた規格値データのヒストグラムであれば、離れたデータがある程度の山の大きさがある原因としては、機械を調整を誤り、その分だけ本来とは異なる分布になった場合が考えられます。

ふた山型

山が二つある分布ができるようになるのは、異なる要因が働いたデータが存在する場合です。

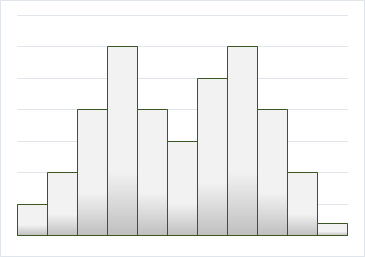
モノづくりをする工場で得られた規格値データのヒストグラムであれば、異なる技術レベルの2人の作業者、2台の機械などの異なるものがデータに影響を与えたと考えられます。

高原型

中心付近の区画の度数に差がなく、山頂が平らになった高原状になった分布です。

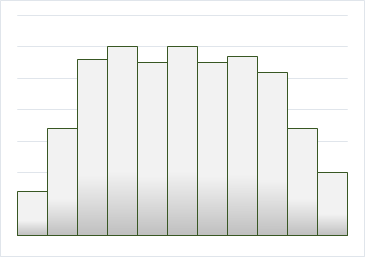
平均値の異なるグループが2つとは限らず、複数混ざり合うとこのような分布になります。

工場で得られるデータであれば、複数の機械、複数の道具、複数の作業者による製品など平均値の異なるグループが混ざり合ったことが考えられます。

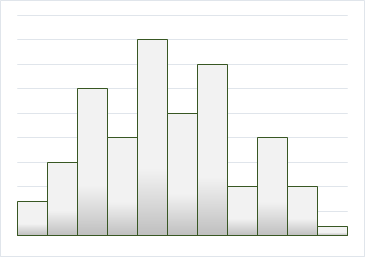
歯抜け型

きれいな山型ではなく、デコボコとしたヒストグラムです。

このような形になる原因は、

• データ数が少ない場合
• ヒストグラムの区間の幅の決め方が悪い場合（幅が狭い）
• 測定器がクセを持っていたり、測定値の読み方が悪い場合

などです。

測定値の読み方が悪いというのは、たとえば定規の数値を読み取るときに、おおざっぱに四捨五入するようにして読んでしまう場合などです。

ゆがんだ型（すそ引き型）

左右のどちらかに、長く裾が伸びた形です。

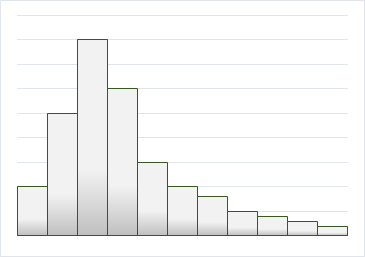
正常な工程であってもこのような分布は発生する場合はあります。その原因は、

• ばらつきについてのデータ
• 片側に制約があるデータ
• 頻度の少ない出来事

などです。

貯蓄額のデータはこの分布になりますね。大きなデータを見ると度数は少なくなりますが上限がありません。一方、データが小さいほうを見ると0円より下は存在しません。片側に制約があるデータといえます。

参考記事　貯蓄額などの裾の長い分布は平均値だけを見ていてはいけない

まとめ

いかがでしたでしょうか。左右対称型、離れ小島型、ふた山型、高原型、歯抜け型、ゆがんだ型を紹介しました。

ヒストグラムは視覚的にわかりやすく、データの分布をパッと見で把握することができます。

また、グラフの形からデータが生まれた背景を読み、ものごとを改善することに役立てることができます。