確率について理解し、理論を展開するためには、確率の基本用語や概念を知っておく必要があります。
確率の概念は、標本空間や事象をつかって考えることができます。
この記事では、確率でつかう基本用語について、また標本空間や事象などについて説明します。
標本空間と事象とは
用語の解説
コインを投げたり、サイコロを振ったりすることを「試行」といいます。
表が出るか・裏が出るかといったような、起こりうる個々の結果のことが「標本点」で、起こりうる全ての結果の集合が「標本空間」です。
その全体の集合を「標本空間」(または「全事象」)といい、Ω の記号であらわされます。
偶然的に起こりうる実験の結果が「事象」。たとえば、サイコロ投げで奇数の目が出る事象であれば、1・3・5 の目の三つがあります。
コイン投げの標本空間と事象
1枚のコインを投げる場合のことを考えてみましょう。結果は、表か裏の2通りしかありません。
コイン投げの標本空間は、
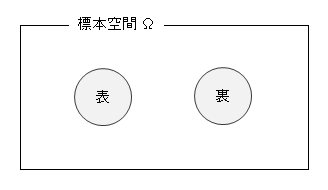
標本空間 Ω={表・裏}
とあわらします。標本空間や事象の理解のために、図が描かれることもあります。
標本空間を長方形であらわし、事象を内部に円で描いたもので、
こんな感じの図です。これを「ベン図」といいます。
サイコロ投げの標本空間と事象
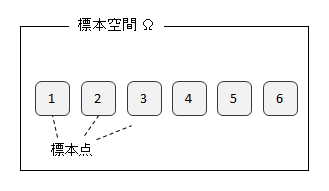
6面のサイコロを投げたときは、1、2、3、4、5、6の目のいずれかが出ることが、起こりうる結果ですから、標本空間をあらわすと、
標本空間 Ω={1・2・3・4・5・6}
となります。
標本点はそれぞれの個々の結果のことを指します。標本空間に含まれる集合が「事象」です。「事象」は標本点一つの事もあれば、複数の標本点が合わさっていることもあります。
たとえば、偶数の目が出る事象であれば、2・4・6 の目が出ることです。
1・2・3 の目が出るという事象もあります。
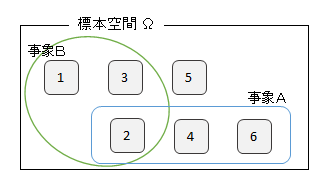
標本空間 Ω={1・2・3・4・5・6}
偶数の目が出る事象・・・事象A={2・4・6}
1~3の目が出る事象・・・事象B={1・2・3}
の場合には、ベン図は、次のようになります。
事象と事象の関係
和事象
事象Aと事象Bのうち少なくとも一つが起きる事象を「和事象」といい、「A∪B」とあらわします。
AまたはB、あるいはA or Bという意味で、記号は「エー・カップ・ビー」読みます。
記号の「∪」の形はコーヒーカップなどのコップの型に見えますよね。AとB両方をコップに入れて合わせてしまうイメージから、英語のCupで、「カップ」と覚えるのがいいでしょう。
積事象
事象Aと事象Bが同時に起きる事象を「積事象」といい、「A∩B」とあらわします。
AかつB、あるいはA and Bという意味で、記号は「エー・キャップ・ビ」ーと読みます。
記号の「∩」は、帽子の形のように見えますから、帽子は英語のCap、そこから「キャップ」と連想できます。
余事象
事象Aが起きない事象のことを事象A「余事象」といいます。
右上に「C」をつけて、「AC」のようにあわらしたり、右上に「 ’ 」をつけて「A’」とあらわします。
事象Aと事象Bが起きない事象の事であれば、事象AまたはBの「余事象」といいます。
「(A∪B)C 」、「(A∪B)’ 」とあらわします。
※Cは、余事象 complementary event の頭文字です。
ベン図で和事象、積事象、余事象を考察する
上にも掲載したベン図を再度掲載します。こちらで考えてみましょう。
事象Aと事象Bの和事象
和事象ですから、事象Aまたは事象Bです。事象AかBのどちらかが起こればよいのです。
上記図では、青線と緑線のどちらかに囲まれた事象ですから、1・2・3・4・6 の目が該当します。
A∪B={1・2・3・4・6}
事象Aと事象Bの積事象
積事象ですから、事象Aかつ事象Bです。事象AとBが同時に起こることを指します。
上記図では、青線と緑線の両方に囲まれた事象です。それは、2 の目だけです。
A∩B={2}
事象Aと事象Bの余事象
余事象ですから、事象Aでもないし事象Bでもないものです。余事象は、青線と緑線のどちらにも囲まれていない事象で
(A∪B)C={5}
となります。