正規分布の形など特徴や性質、確率密度関数の式と表す記号について説明します

正規分布は、統計学で学ぶ分布のなかでも、よく目にする分布、もっとも重要な分布です。

正規分布の形、確率密度関数の式と表す記号などに正規分布の基本について説明します。

正規分布の形

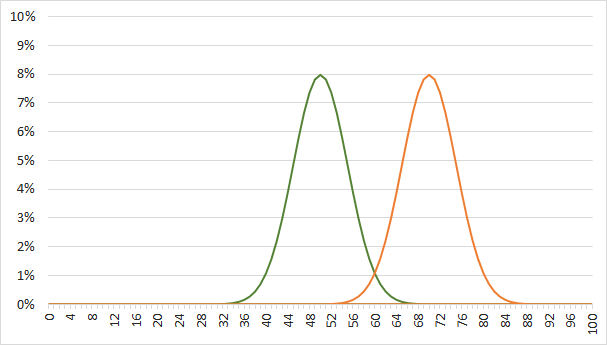
正規分布は、中央が一番頻度が大きく、左右対称で滑らかで美しい形をしています。平均値＝中央値＝最頻値が同じ値になっており、中心から離れるに従って、下の線に近づいていく、釣鐘や富士山の形にカーブした分布です。

ヒト（成人）やそのほか動物の身長、学校のテストの成績、製品のサイズなどなど、多くの自然現象や社会現象は、正規分布に近い形をとります。正規分布に近似するといい、近似しているのであれば、実用上、正規分布として取り扱うことができます。

正規分布の確率密度関数

確率密度関数の式は、次のとおりです。

$$f(x) = \frac{1}{\sqrt{2\pi}\sigma^2}\exp \left( -\frac{(x-\mu)^2}{2\sigma^2} \right)\ \ (-∞<x<∞)$$

正規分布を表す記号

平均値が$μ$、分散が$\sigma^2$である正規分布は、

$$N(μ，\sigma^2)$$

または、

$$X～N(μ，\sigma^2)$$

と表記されます。$X～$は、確率変数$X$は平均$μ$、分散が$\sigma^2$の正規分布に従うという意味です。

$N$はNormal distribution（正規分布）の頭文字です。平均値と分散で表記されることになります。

成人男性の平均身長が170ｃｍ、分散が25ｃｍ（標準偏差5ｃｍ）とすると、

$$X～N(170，5^2)$$

または

$$X～N(170，10)$$

とあらわします。

分散や標準偏差については、こちらの記事を参考にしてください。

参考記事　分散と標準偏差の意味と計算方法

世の中には正規分布するものごとが多い

なにか製品をつくるときのことを考えてみましょう。

たとえば割りばし。製品は設計段階において規格値が定められます。割りばしであれば、長さ21cmの割りばしをつくろうと決めて、それができるように製造機械の設定・調整をするはずです。

でも、すべての割りばしがピシャリと21cmになるわけではありません。21.1cmやら20.9㎜の割りばしもつくりだされます。一見21.0cmとみられた割りばしであっても、もっと精密に計測できる機器を用いれば、21.01cmのようなサイズなっているわけです。

出来上がる製品サイズは、ねらったサイズから多少誤差が生まれてしまうのですが、見た目にはわかりませんし、実用上まったく問題ありませんので、そのまま製品化されます。

誤差が生じてしまうとはいっても、目標としている規定のサイズ、つくろうとねらっているサイズがあるわけですから、当然その規定サイズ付近の製品が一番多くつくられます。21cmから少しだけサイズがズレた製品は多くつくられ、ねらいのサイズからとんでもなく大きいサイズや大きすぎるものや小さすぎるものは、よほどの失敗をしないと作られませんから、少ないはずです。

このように、目標の規格値どおりの製品をつくりだそうとすると、目標値が平均値となり、目標値付近の製品がたくさんつくられ、目標値から離れるほど少なくなるので、上記したグラフのような分布をするはずです。ものづくりの製品サイズや重量の値などは正規分布に近似します。

このように誤差があることによって、正規分布に近い分布になるのです。そのため正規分布は誤差曲線とも呼ばれます。

学校のテストの成績はどうでしょうか。

ずば抜けて成績の良い学生、逆に全く勉強しないとても成績の悪い学生は、双方とも少数派です。多の学生が平均点付近やあまり離れていない点数を取り、ずば抜けて良い成績をとれる学生の数は少なく、とても成績が悪い学生も少ないですよね。

こちらも、平均値を中心にして裾にいくほど数が少なくなるような分布をし、正規分布に近い分布となります。

ものづくりの製品、テストの成績、人の身長、動植物の体長などなど、世の中には正規分布があふれています。

正規分布の特徴。正規分布は平均値と分散・標準偏差で決まる

正規分布は、平均値と分散（または標準偏差）でどのような分布になるのかが決まります。

平均は分布グラフの中央の値の大きさ、分散は山の広がり具合です。

上記したように、平均値が$μ$、分散が$\sigma^2$である正規分布は、

$$N(μ，\sigma^2)$$

と表記されます。

分散・標準偏差の値が小さければ、急峻な岩山のような形になり、分散・標準偏差の値が大きければ、裾が広がったのっぺりとした丘のような形になります。

分散と標準偏差は同じようなものですから、ここでは標準偏差のほうをとりあげて話を進めていきます。

平均値の$μ$、標準偏差の$\sigma$。この2つの値が決まれば、正規分布がどんな形をするのかも決まってしまいます。ですから、$N(μ，\sigma^2)$とシンプルに表記されることになります。

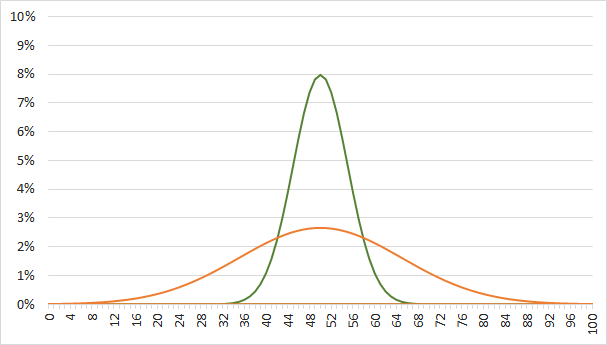
平均値は同じで、標準偏差を変化させた分布

2つの正規分布をグラフにしました。

平均値は同じく50で、標準偏差を5 、15 と変化させたグラフです。

標準偏差が小さいほど、グラフの山は急になり、

標準偏差が大きくなると、分布のてっぺんの位置は同じままで、山がのっぺりと広がります。

緑色： N（50，5²）

オレンジ色： N（50，15²）

標準偏差は同じままで平均値を変化させた分布

今度は、標準偏差をそのままにして、平均値を変化させてみました。

標準偏差は同じく5 ですが、平均値を50、70 と変化させたグラフです。

標準偏差は同じであればグラフの山の形はそのままで、平均値が大きくなると山の位置が右へスライドします。平均値が小さくなると山の位置が左へスライドします。

緑色： N（50，5²）
オレンジ色： N（70，5²）