HARMEAN 関数は、調和平均を計算することができる関数です。
調和平均を英語でいうと「HARMONIC MEAN」です。これを略してHARMEAN となったのでしょう。
調和平均とは
調和平均とは、時速などを計算するときに使う平均値です。調和平均の理解がある方は、読み飛ばしてください。
ドライブに行って、行きは平均時速80㎞、帰りは平均時速30㎞のスピードで走行したとしましょう。
単純に算術平均で計算すると、
(80 + 30 )/ 2 = 55
時速55kmとなります。しかしこれは誤りで、帰りのほうが遅いぶん時間をかけて走っているのだから、影響が大きくなるはずです。
こんなときは、調和平均をつかって計算をします。
\(\frac{1}{調和平均x_H}\)は、逆数どうしの算術平均として定義されています。
$$\frac{1}{x_H}=\frac{1}{n}(\frac{1}{x_1}+\frac{1}{x_2}+…+\frac{1}{x_n})$$
※Hは、調和平均の意味である harmonic-mean の頭文字です。
※算術平均とは、ふつうの平均というか、一般的によく使われる、データの和をデータの個数で割ったもの
数式を変化させて、
$$x_H=\frac{1}{\frac{1}{n}(\frac{1}{x_1}+\frac{1}{x_2}+…+\frac{1}{x_n})}$$
この数式に当てはめれば、同じように
$$x_H=\frac{1}{\frac{1}{2}(\frac{1}{80}+\frac{1}{30})}$$
$$=43.636km$$
となります。
参考記事 調和平均の意味と計算方法
エクセルのHARMEAN 関数をつかった調和平均の計算方法
行きは平均時速80㎞、帰りは平均時速30㎞のスピードで車でドライブしたとします。この行き帰り合わせた全体の平均時速は何kmでしょうか?これをHARMEAN 関数で計算してみます。
セルに
「= HARMEAN( )」
を入力し、
「= HARMEAN(数値、またはデータ範囲)」
データ範囲を指定します。この例では、時速○○km/h のデータを指定します。調和平均の値が計算され表示されます。

行きと帰りの時速を指定します。
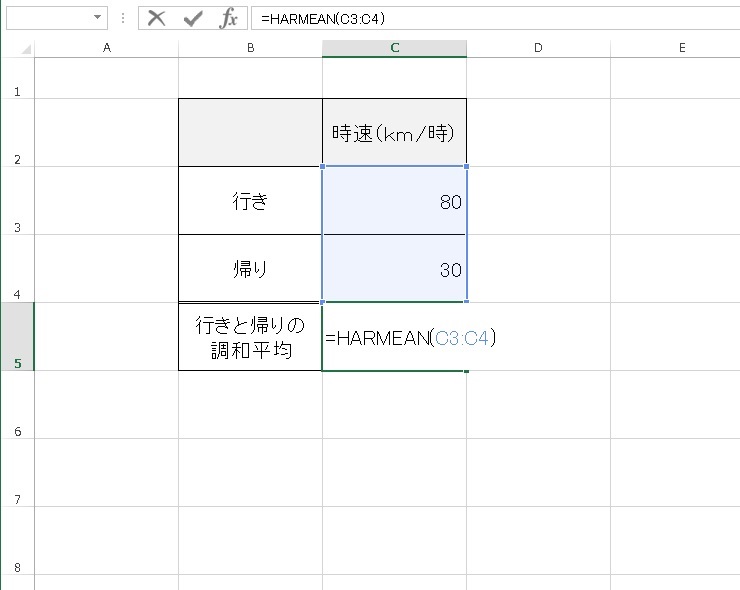

時速は 43.636km となりました。