エクセルで分散を計算する関数として、VAR.S とVAR.P の2つがあります。
両方とも分散を計算する関数なのですが、お尻についた「S」と「P」によって計算結果が変わってきます。
その違いについて説明していきます。
VAR.S とVAR.P の違い
VAR.Sは、母集団から抜き取った標本のデータを用いて、母集団の分散を推定する場合につかいます。
VAR.Pは、母集団全体のデータを用いて母集団の分散を計算する場合につかいます。母集団のデータが100個であり、その100個をすべて得て分散を求めるのであればこちらを使います。
母集団と標本の意味については、こちらの記事に書いています。
参考記事 母集団と標本の意味とその違い
エクセルでVAR.S/VAR.P 関数を使った分散の計算方法
VAR.S 関数を使う場合
VAR.S 関数をつかうのは、計算につかうデータが標本データの場合です。
他のページで、共分散を計算するCOVARIENCE 関数について書いておりまして、そこで母集団と標本について説明していますので、引用します。
COVARIENCE 関数で共分散の計算をするときの考え方について書きましたが、共分散を→分散として読み替えて、参考にしてください。
メメーカーで、とある製品を毎日毎日つくり続けているとします。30個ぶん、この製品のサイズ・重量をはかって、それらの共分散を計算するときのことを考えてみましょう。
メーカは、この製品をずっとつくり続けてきており、これからもつくり続けます。
ある日、30個だけのサイズと重量をはかるといっても、その30個についてだけを知りたいのではありません。ずっとつくり続けている製品すべてのサイズ・重量について知りたいのです。
そのような調査対象全体のことを母集団といいます。
過去から未来にかけてのすべての製品が母集団となるでしょう。こういった、数は無限であると考えられる母集団は、無限母集団といいます。
製品30個は、その無限母集団から取り出した一部分であり、これが標本です。
母集団から取り出した一部分(この場合であれば30個)の分散を計算するなら、VAR.S をつかいます。
VAR.S の「S」は、sample(標本)の「S」で、英語で言うと母集団はpopulationです。VAR.P の「P」は population の「P」でしょう。
- 標本のデータで計算し、母集団の分散を推定するならVAR.S を使います。
- 母集団全体のデータで計算し、母集団の分散を求めるならVAR.P を使います。
標本のデータで分散を計算するときでも、私たちが知りたいのはあくまで母集団全体の分散ですよね。標本のデータは母集団の一部を抜き取ったものであり、標本のデータを用いて分散を計算する場合には問題点があります。
それは母集団全体のデータをつかって計算した分散よりも、標本のデータをつかってで計算した分散のほうが値が小さくなってしまいやすいことです。
そこで役立つのが、VAR.S 関数です。
VAR.P 関数で出した値よりも、VAR.S 関数で出した値のほうが大きくなります。(標本のデータをそのまま計算した分散は小さくなってしまいやすい。VAR.S 関数をつかうと値が大きくなって補正されます。)
標本のデータをつかってVAR.S 関数で分散を求めるということは、母集団の分散を推測するという意味あいになります。
なぜ、母集団の分散と比較して、標本の分散が小さい値になりやすいのか、こちらの記事で書いていますので、参考にしてください。
参考記事 母集団の標準偏差の不偏推定値を計算するときに√n-1で割る理由
VAR.P 関数を使う場合
一方で、VAR.P 関数をつかうのは、計算につかうデータが母集団全体のデータの場合です。
ある高校で学生300人分の身長・体重を測定したとします。この300人のデータの特性を知りたいという考えであれば、母集団が300人だということになります。
得られたデータが母集団全体のデータであるときには、VAR.P 関数をつかいます。
使用したデータで、そのまま分散を計算します。
データ数が多ければ、PとS、どちらを使ってもいい
データ分析をする際には、母集団すべてのデータを集められることは少ないはずです。標本を集めて、母集団の特性を推定することが多くなるので、VAR.S 関数を選ぶ場面のほうが多いでしょう。
ですが、データが多いのであれば、結局どちらをつかってもよくなります。
なぜなら、データが多くなればなるほど、結果に差がほとんど出なくなるからです。
データの数が少ない場合
とある10人の身長と体重のデータがあります。この10人が標本のデータであり、母集団のデータの数がもっと多いとします。
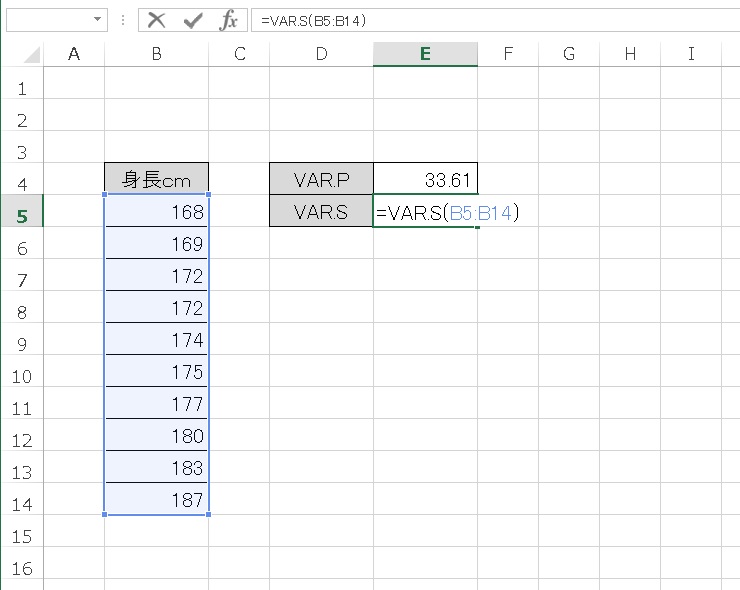
分散をVAR.P 関数、VAR.S 関数で計算してみましょう。
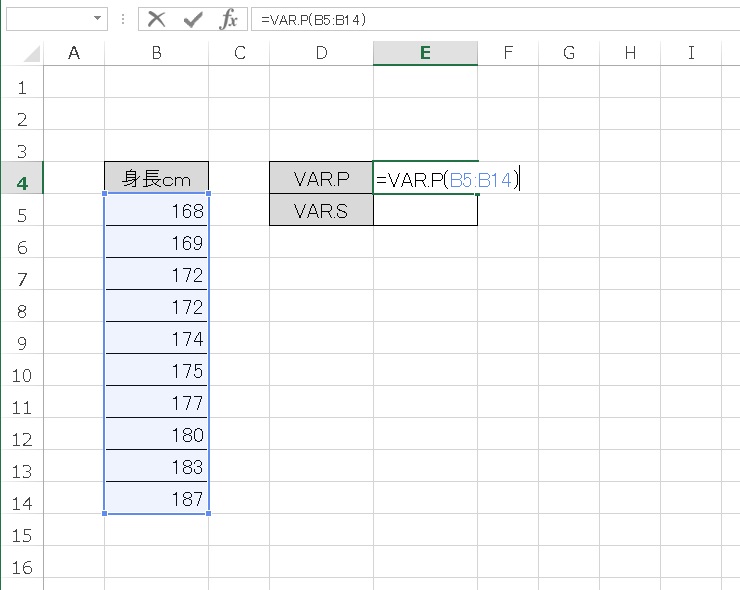
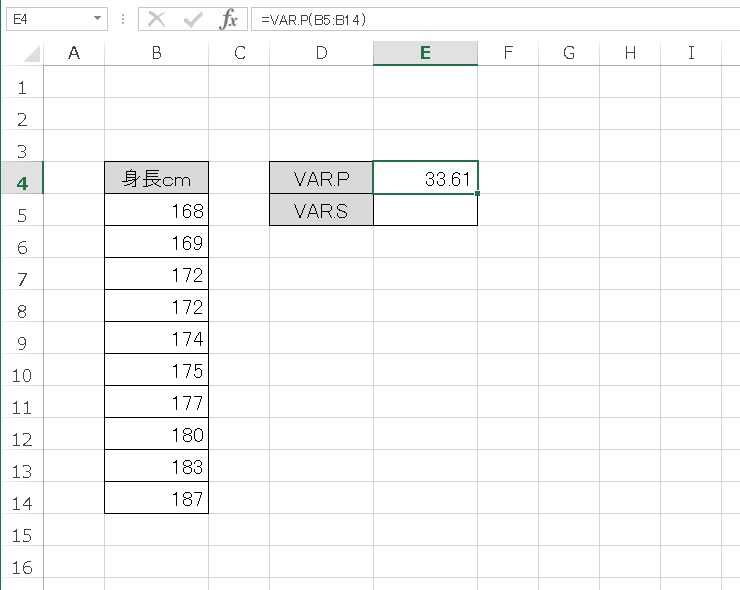
- VAR.P → 33.61
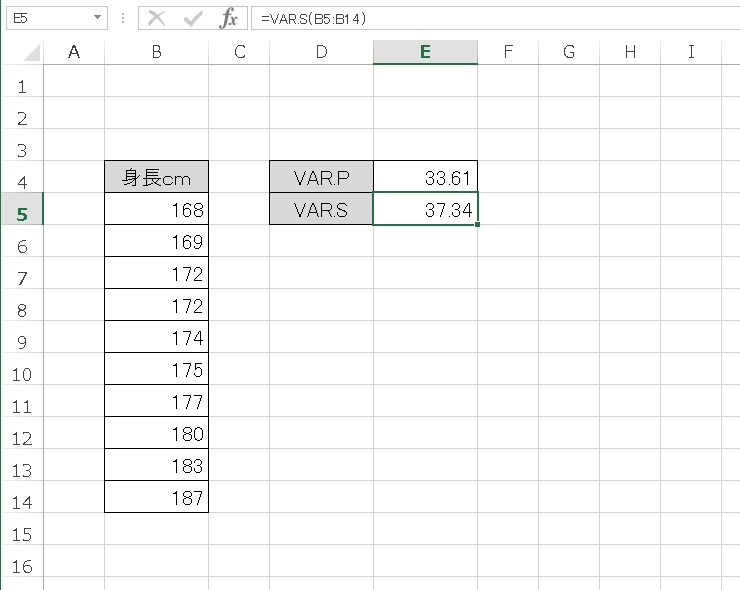
- VAR.S → 37.34
VAR.P 関数のほうが小さな値、VAR.S 関数のほうが大きな値になりました。
VAR.P 関数は、データをそのままつかって分散の値を計算しています。
この10人が標本のデータであり、母集団のデータの数がもっと多いです。
標本の分散は、母集団の分散よりも小さな値になりやすいです。
つまり、10個のデータをそのままつかうVAR.P 関数で算出した33.61 の値よりも、(実際のデータはないですが)母集団全体の分散のほうが大きな値になっている可能性が高いです。
VAR.S 関数で算出した37.34 の値は、補正されて大きな値になっており、こちらのほうが母集団全体の分散に近いだろうと推測できるのです。
データの数が多い場合
データ数を増やして100人の身長・体重データ(エクセルでランダムにつくったデータ)で計算すると、データ掲載は割愛しますが、
- VAR.P → 37.99
- VAR.S → 38.38
となりました。0.39の差しかありませんね。さらにデータが増えれば、ほとんど差がなくなっていきます。
VAR.P 関数とVAR.S 関数で計算結果の数値に違いはあるのですが、ほんのわずかな数値の違いなので、データ数が多い場合は、どちらをつかってもいいかと思います。
ただし、標本のデータ個数がほんとうに少ないときに、分散を計算する場合は、VAR.S 関数をつかったほうがよいです。