GAUSS 関数とは、標準正規分布で、平均からz値までの間の累積確率を計算する関数です。
別の言い方をすると、母集団からランダムに取りだしたあるデータが、平均値から標準偏差z倍の範囲に入る確率を計算する関数です。
z値とは
あるデータの値が、平均値から標準偏差なん個分離れているか?をあらわす数値をz値といいます。
平均値を0、標準偏差を1 に変換して考える方法で、これを基準化とか標準化といいます。
あるデータが平均値から標準偏差1個ぶん離れているのなら、それはz値=1 となります。
正規分布は別名、ガウス分布とも呼ばれます。GAUSS(ガウス)とはドイツの数学者の名前です。
正規分布の基準化変量z(標準化変量)
正規分布と標準偏差について説明します。すでに理解のある方は読み飛ばしてください。
正規分布は、平均値と標準偏差でどのような分布になるのかが決まります。分布グラフの中央が平均値となり、山の広がり具合が標準偏差です。
参考記事 正規分布の基本
正規分布の母集団から、あるひとつのデータを取り出したときに、そのデータは、分布のどこに位置するか、確率的に決まっています。
正規分布は次のような形をしています。
中心が平均値となります。その平均値付近にデータが多く、平均値から離れて大きな値になるほど、または小さな値になるほど、データは少なくなっていきます。
世の中のものごとは、正規分布に近似することがあります。生物の大きさなどに見られます。
正規分布では、分布のちょうど中央が平均値で、そこから標準偏差何個分の範囲に、どのくらいのデータが分布するかということが、確率的に決まっています。
正規分布の母集団があって、ある1個のデータを取りだしたら、
- 68.26%の確率で、平均値から標準偏差 ±1 個分の範囲に入ることがわかっています。
- 95.44%の確率で、平均値から標準偏差 ±2 個分の範囲に入ることがわかっています。
標準偏差は、記号で示すと“σ”です。標準偏差1 個分なら、1σ です。標準偏差2 個分なら、2σ です。

たとえば、男性の身長は正規分布に近い分布です。厳密にいうと正規分布ではないのですが、正規分布として取り扱って考えてみます。
日本人の成人男性の身長は、年齢によって変わりますが、ここでは、
- 平均が171.0cm
- 標準偏差が5.5cm
としましょう(正しい数値ではありません。例題としてつかうため、仮に設定した数値です)。
日本人の成人男性の68.26%は、身長が平均値から ± 標準偏差1個分の範囲(171.0cm ± 5.5cm)になります。
(ランダムに日本人の成人男性を一人選んだら、その人の身長は、68.26%の確率で、171.0cm ± 5.5cmの範囲になります)
日本人の成人男性の95.44%は、身長が平均値から ± 標準偏差1個分の範囲(171.0cm ± 2 × 5.5cm)の範囲になります。
(ランダムに日本人の成人男性を一人選んだら、その人の身長は、95.44%の確率で、171.0cm ± 2× 5.5cm の範囲になります)
次に、平均値からプラスマイナスで考えるのではなくて、プラス方面だけに考えてみましょう。上記の半分にすればOKです。
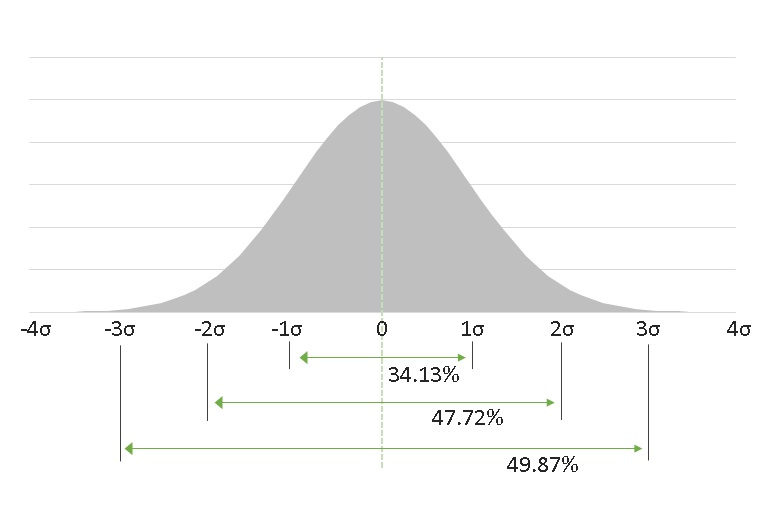
- 34.13%の確率で、平均値から標準偏差 プラス側 1 個分の範囲に入ります。
- 47.72%の確率で、平均値から標準偏差 プラス側 2 個分の範囲に入ることがわかっています。
あるデータの値が、平均値から標準偏差なん個分離れているか、あるいは何倍離れているか?をあらわす数値をz値といいます。
平均値を0、標準偏差を1 に変換して考える方法で、これを基準化とか標準化といいます。また、平均値を0、標準偏差を1 に変換した正規分布のことを、標準正規分布と呼びます。
あるデータが平均値から標準偏差1個ぶん離れているのなら、それはz値=1 となります。
参考記事 基準化の意味と基準化変量の求め方(標準化ともいう)
z値をつかって、平均値からz値までの累積確率を計算することができるのが、GAUSS 関数です。
GAUSS 関数で確率を計算する
GAUSS 関数は、平均値からz値までの累積確率を計算します。
言い換えると、母集団からランダムに取りだしたあるデータが、平均値から標準偏差z倍の範囲に入る確率を計算します。
例として、日本人の成人男性の身長が正規分布しているとして、
- 平均が171.0cm
- 標準偏差が5.5cm
として、計算をしてみます。
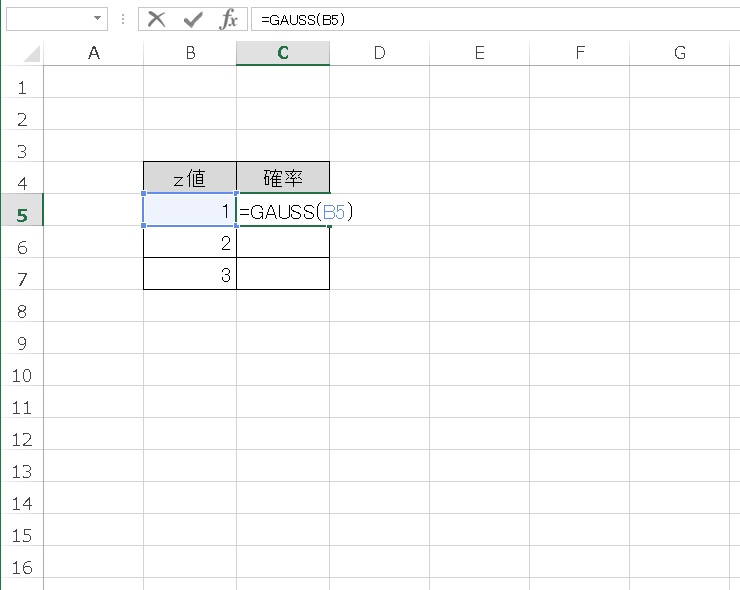
セルに
「= GAUSS( )」
を入力し、
「= GAUSS(z値)」
z値を指定すると、正規分布で、平均値からz値までの累積確率を計算します。
z値の指定は、直接数字を入力してもいいですし、数字を入力した他のセルを指定してもいいです。
ここでは、z値=1、z値=2、z値=3 のときに、平均値からそのz値までに入る確率を見てみます。
※z値=1 ということは、平均値から標準偏差1個分までの累積確率を計算します。
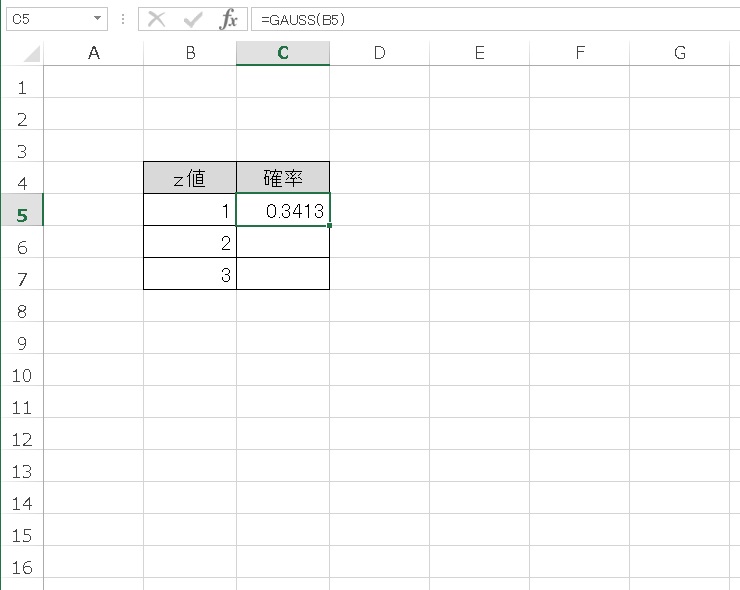
平均値からz値=1 までの累積確率は、0.3413 です。
さらに、z値=2、z値=3 のときも見てみます。
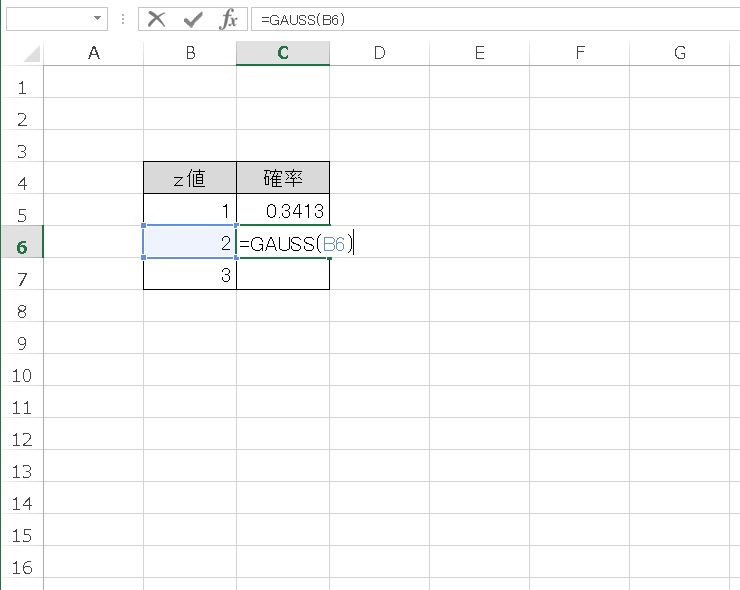
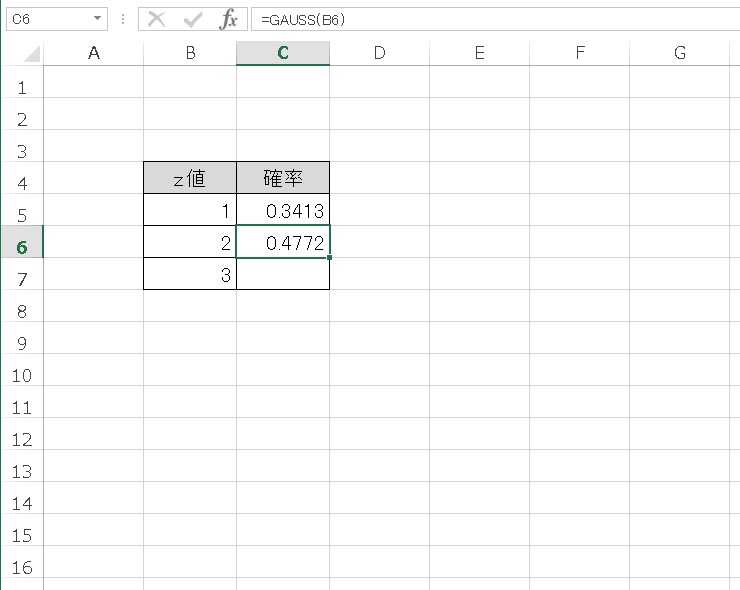
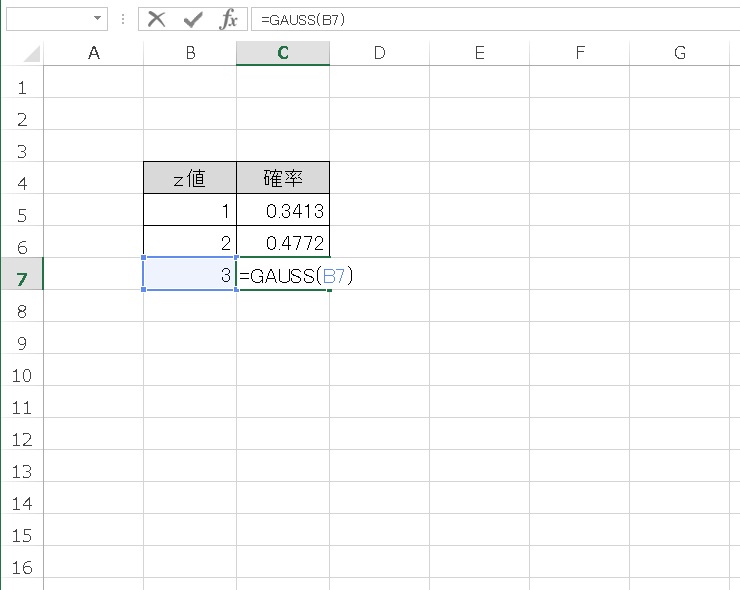
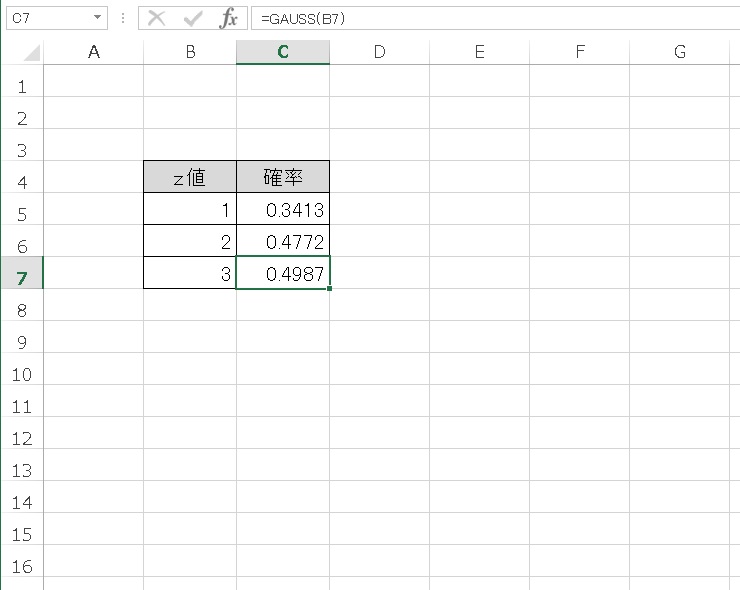
平均値から標準偏差2個分までは、0.4772 、平均値から標準偏差3個分までは、0.4987 の累積確率となりました。
さきほどの身長の話でいうと、
日本人の成人男性の47.72%の人たちの身長は、平均身長の 171.0cm から標準偏差2個分( 2 × 5.5cm)の範囲になる、ということです。
(ランダムに日本人の成人男性を一人選んだら、その人の身長は、47.72%の確率で、平均身長の 171.0cm から標準偏差2個分( 2 × 5.5cm)の範囲になるといえます)
ところで、私の身長は、175.0cm。この身長で計算してみましょう。
175.0 - 171.0 = 4.0cm
偏差は4.0cmとなります。そして、偏差4.0cmを標準偏差5.5cmで割ると、
4.0 / 5.5 = 0.7272…
です。
基準化変量z=0.7272です。標準偏差0.7272個分です。

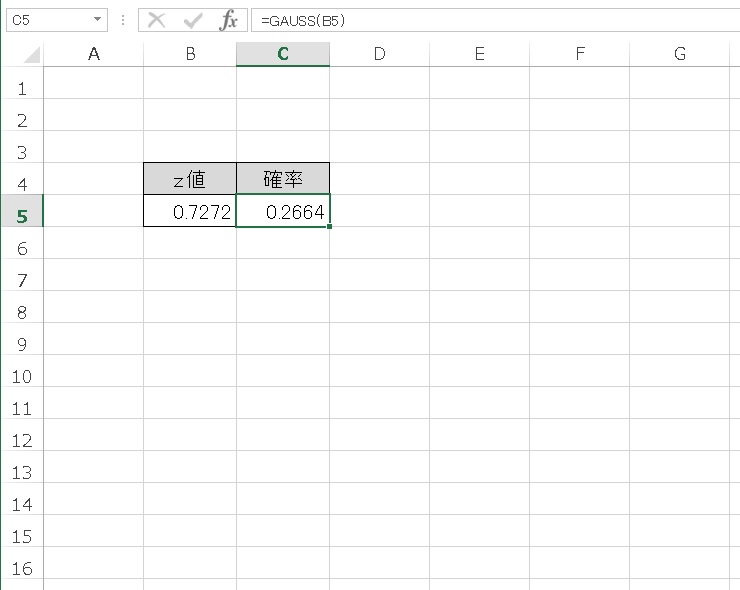
日本人の成人男性の26.64%の人たちの身長は、平均身長175.1cmから私の身長175.0cm の間になるようですね。
私の身長175.0cm以上、また以下の確率も計算することができます。
平均値以下は、0.50 の確率ですから、175.0cm以下の人の割合は、
0.2664+0.5000=0.7664
76.64% であるといえます。175.0よりも大きい人は、
1.00-0.7664=0.2336
23.36% の割合でいるので、175.0cmは、平均よりも高い身長ですが、分布のなかではそんなに大きいわけではないなと、わかります。
といった具合に、GAUSS 関数を用いることで、z値をつかって正規分布のどこに位置するのかといったことが、わかるようになります。