相関関係は非常に便利なもので、2つのデータに関係性があるかどうか、問題の原因を特定し、解決策を考案することができたりします。相関関係を見るときには散布図をつくることになります。ここで、注意をしなければならないことは、
- 相関関係がないのに、あるように見えてしまうこと
- 相関関係があるのにないように見えてしまこと
です。これらはデータの混在やデータの切り捨てによって起こりえます。
データの混在による相関関係の錯覚
相関が無いのにあるように見えてしまう
身体が大きいほうが、英語力があるということを示す散布図があったとしましょう。中学生の身長と英語力の散布図です。

パッと見では、相関関係があるように見えます。
身長が高い方が、英語力もありそうです。ですが、これは違いますよね。
中学生が成長期にあり、1年がたって学年が上がれば身長もずいぶん伸びますし、英語の勉強も進みますので英語ができるようになります。当然、中学1年生から3年生へ成長すれば、身長も英語力も成長するに決まっているので、こういったデータをとってもあまり意味がありません。
- 中学1年生の身長と英語力
- 中学2年生の身長と英語力
- 中学3年生の身長と英語力
をそれぞれ調べるのです。そうすると、下記のような散布図ができあがりました。
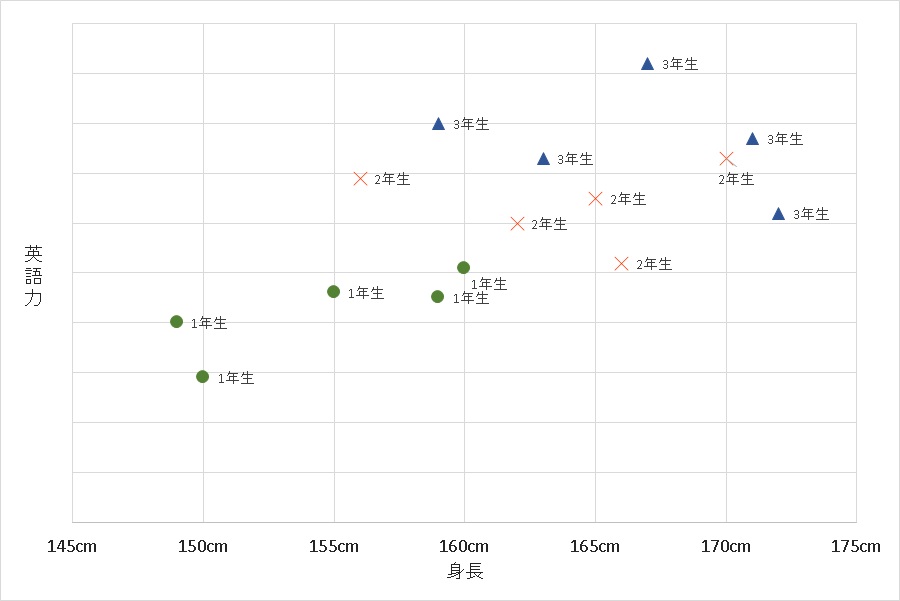
中学1年生~3年生のデータを混在させると、あたかも相関があるように見えましたが、各学年でみるとそうでもなさそうですね。
データをとって身長と英語力の関係を見たいのであれば(相関はなさそうですが)、各学年のなかでの身長と英語力の相関を見たほうがよいです。
もっといえば、学年でひとくくりにするのでなくて、生後13年と1ヵ月、13年と2ヵ月といったように月単位で見るべきでしょう。
ひと学年のなかでも、早生まれなのか、遅い生まれなのかによって、身長差には差が出てきます。4月生まれなのか、3月生まれなのかは、ほとんど1年の違いがありあすよね
相関があるのに無いように見えてしまう
年功序列で賃金が上がっているかどうか、ある会社の従業員の年齢と収入の関係を見てみます。
年齢ごとに各人の収入を見ると、下記のようなグラフができあがりました。
相関がなさそう。
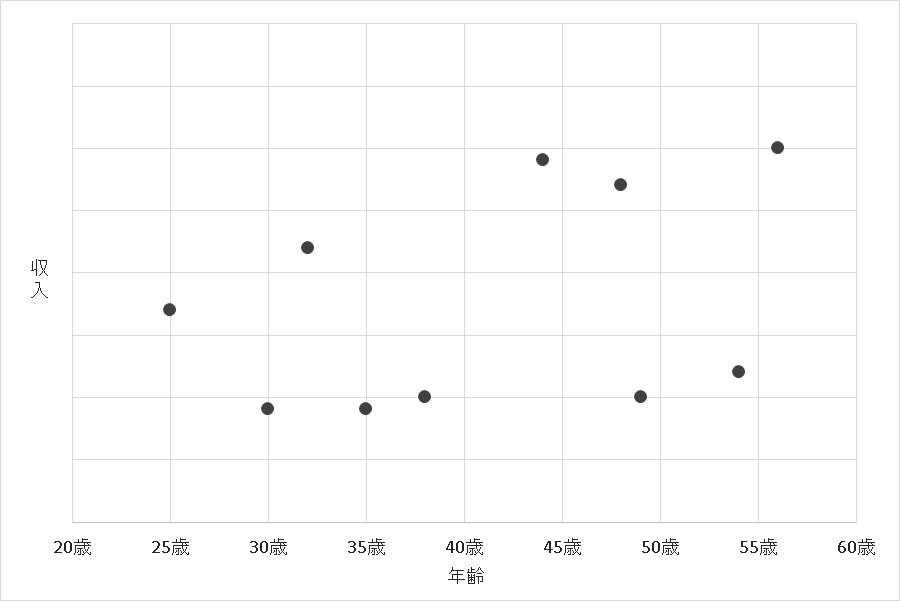
実はこのデータには、パートと正社員が混在していました。
上記の散布図を見るかぎり、相関関係がないように見えてしまいますが、パートと正社員を分けて見てみることで、パートは上がりにくく、正社員は年を重ねるごとに上がっていそうだなとわかります。

このように異質なデータを混在させると、本当は相関があることなのに、相関がないように見えてしまいます。
層別すると意味のある情報が取り出せることがあります。
データの切り捨てによる相関関係の錯覚
相関がないのにあるように見えてしまう
若者には車離れがあると言われます。
車持っているかどうか、欲しい車があるかなどをアンケート調査し、車に関する関心度を測りました。その結果、
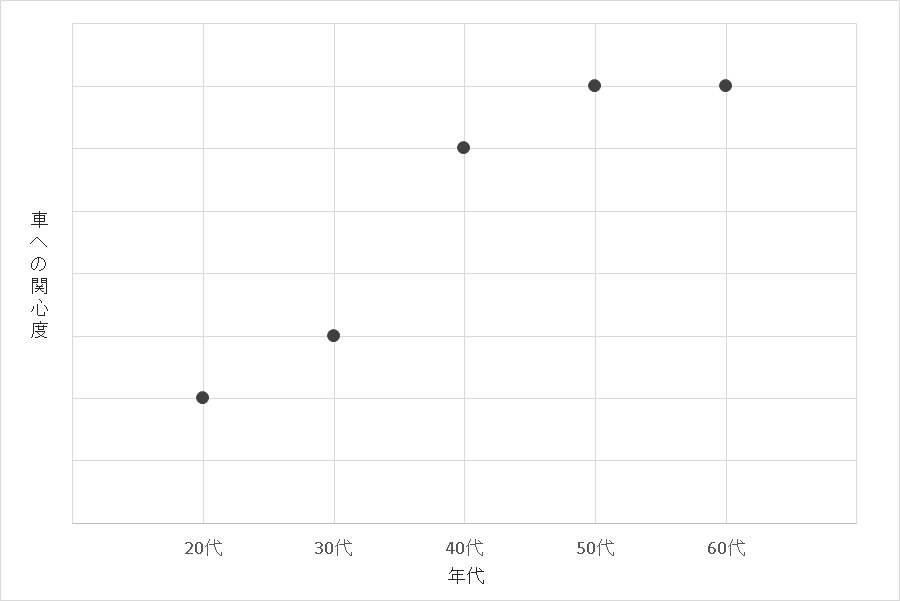
これだけ見ると、若い年代ほど車を持っていないし、車への関心もなさそうに見えます。
しかし。この調査は東京にあり、身近な東京都民にだけ、アンケートをとった結果なのでした。
東京から離れた地方に住む人は、車を持つ人が増えるでしょう。日常生活の足として必要となるからです。車が無ければ仕事場に行ったり、買い物に行ったりするのもひと苦労も、ふた苦労もする地域もあるでしょう。そういう意味では車に関心もあります。
東京から離れた地方の人にもアンケートをとって車への関心度を測ってみると、
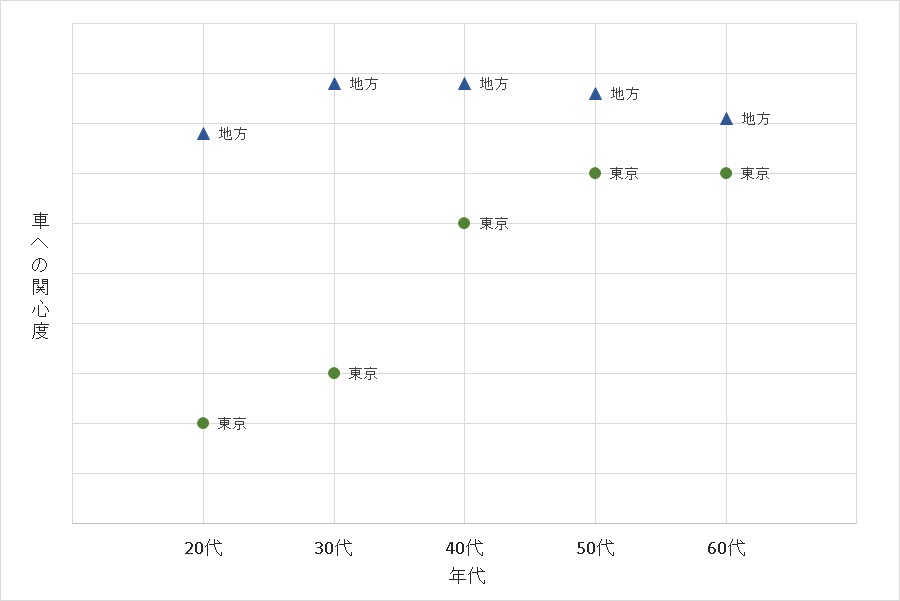
このような散布図になりました。強い正の相関はなくなりました。
相関があるのにないように見える
企業が新卒採用を行うときには、学歴を見ます。
たしかに、大学の入学試験でよい成績をおさめたことは、それだけの記憶力や情報処理能力があることを示していますし、大学受験のための勉強によって猛烈に頭をつかったことによって、頭が鍛えられているでしょうから、評価基準としては理にかなっています。
今は、学歴を伏せた状態で採用活動を行う企業もあると聞いたことはありますが…。
ある企業では、「学歴」と「新卒の入社後の仕事能力・仕事ぶり」を調べてみました。学歴には1~5段階の評価を与えています。
「学歴」と「新卒の入社後の仕事能力・仕事ぶり」相関関係はなさそうだ、と結果が出たとしましょう。だから、入社試験では、学歴を重視する必要はないのではないかという結論が導かれました。
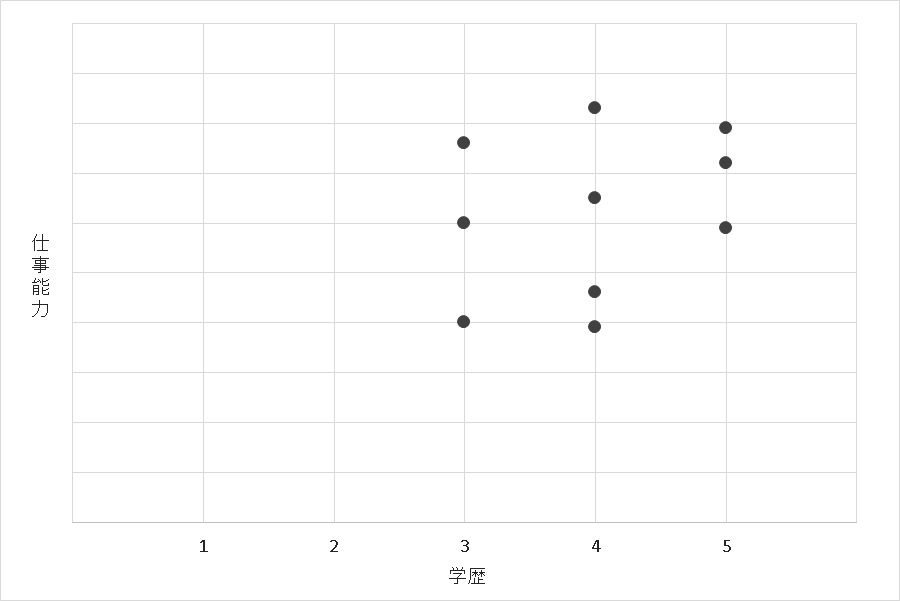
しかし、この散布図には載っていませんが、もともと学歴を重視していたこの企業には入社できなかった人たちがいます。学歴によって、足切りされてしまった人たちです。
上記の散布図は、一定以上の学歴を持った人たちだけのデータでつくられたものであって、もし足切りされてしまった人たちが入社していて、学歴と仕事能力の散布図をつくったのであれば、ひょっとしたら次のような散布図ができあがるかもしれません。
こうなる
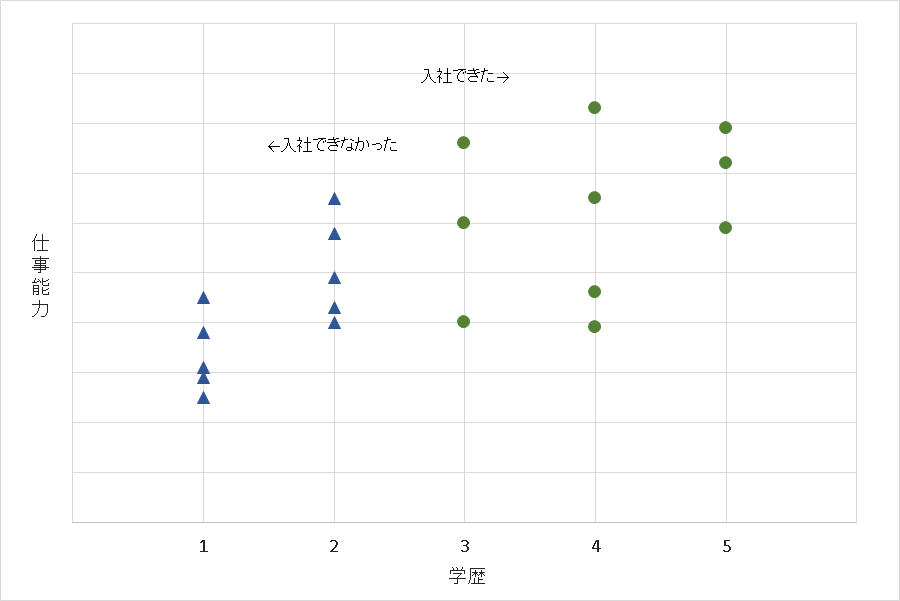
右肩上がりになっていて、相関がありそうです。
実は学歴と仕事能力にはきちんと関係があって、学歴も採用基準のひとつにしておいたほうがよい、といえるのかもしれません。
まあ、それはやってみないとわからないのですが…。ただ、言えることは、切り捨てられたデータも含めて散布図を見てみない限りは、ほんとうに学歴と仕事能力に関係があるかどうかの結論は出せないということです。今いる社員の学歴のなかでは、学歴と仕事ぶりは関係ないと、結論づけることはできますが…。
混在と切り捨てに注意
- 混在しているデータがあるとき
- 切り捨てられたデータがあるとき
注意が必要です。
- 相関関係があるのにないように見えること
- 相関関係がないのにあるように見えること
がありえます。
散布図を書いて相関関係があることを発見は、問題解決への重要な手がかりになることが多いですが、そこで見出した相関関係は使いものにならない場合もあるのです。
相関を調べたら、なぜ相関があるのか、混在しているデータや切り捨てられたデータがないか考えること。また、相関関係があれば因果関係があるわけではありません。これらのデータには因果関係はあるのかどうかを考えるころ。
さらに、その因果関係を検証するために、データを集めて検証を行っていく。こういった姿勢を持つことで相関関係を活かして問題解決をしていくことができるようになります。