検定には、棄却域を分布の両側に設定する検定と、片側だけに設定する検定があります。前者が両側検定で、後者が片側検定と呼ばれます。
両側検定
母平均の検定を行うときのことを考えて説明します。母平均がμ0であると設定したときに、両側検定とは、
- 帰無仮説 H0: μ = μ0
- 対立仮説 H1: μ ≠ μ0
この帰無仮説を設定し、検定統計量の分布において、棄却域を分布の両側に設定する検定です。平均値が大きいか小さいかわからない、または大きいことと小さいことも問題にするような場合には、両側検定を行います。

図のように、棄却域を両側に分布の設定します。有意水準5%であれば、左側の棄却域は2.5%の範囲、右側の棄却域は2.5%の範囲となり、合わせて5%です。
たとえば、充電をしなくても平均100時間使用し続けることができるスマホ商品があったとします。
本当に100時間なのかどうか検定する場合は、両側検定になります。100時間以上、使用できるのであればいいかもしれないですが、ここで検定したいことは、平均100時間と謳われた商品が本当に平均100時間もつのかどうかです。
- 帰無仮説 H0: μ = 100
- 対立仮説 H1: μ ≠ 100
と、仮説を立てます。
片側検定
上記と同じく、母平均の検定を行うときのことを考えて説明します。母平均がμ0であると設定したときに、片側検定とは、
- 帰無仮説 H0:μ = μ0
- 片側対立仮説 H1:μ > μ0
または H1:μ < μ0
この帰無仮説を設定し、検定統計量の分布において、棄却域を分布の片側だけに設定する検定です。
小さいほうだけ、または大きいほうだけを問題にする場合には、片側検定をします。
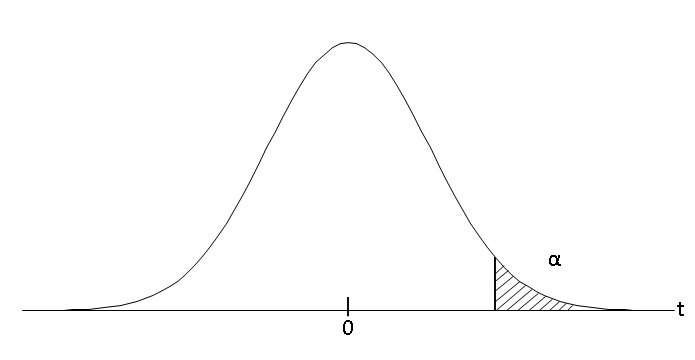
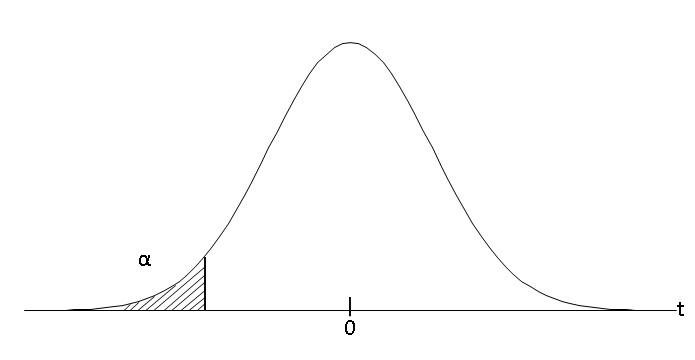
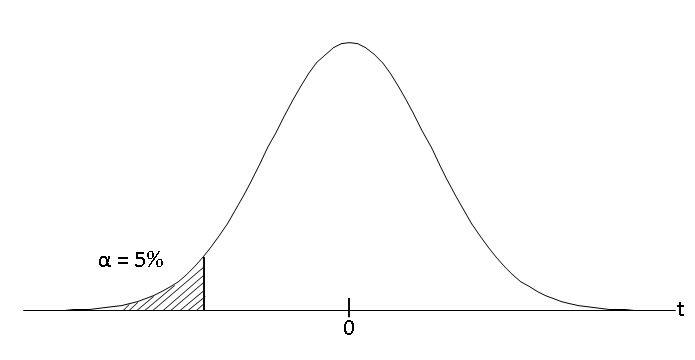
図のように、棄却域を分布の片側に設定します。小さいほうに設定する場合もあれば、大きいほうに設定する場合もあります。
有意水準5%であれば、片側だけの棄却域で5%の範囲となります。
上記した100時間充電無しで使えるスマホ話を少し変化させてみます。
「100時間からさらに長持ちするようになりました」と謳った新しいスマホ商品があれば、消費者側から見ると、ちゃんと100時間からさらにのびているのか気になりますよね。
そこで検定するとしたら、100時間より長くなっているかどうかを検定します。
この場合は、仮説として、
帰無仮説 H0: μ = 100
対立仮説 H1: μ > 100
を立てて、片側検定を行います。
片側検定の進め方
続けてもう少し片側検定のことを書いていきます。
仮説の立て方
とある開発者が、長持ちする電池を新たに開発しました。これを普及させていきたいと考えています。
このときに開発者として興味があるのは、従来の電池と比較して、新しい電池が長持ちするかどうかですよね。
実験によって、長持ちがどうか検定をすることにしました。新しい電池の寿命をμ1 、従来の電池の寿命をμ0 とすると、両側検定の場合は、
- 帰無仮説 H0: μ1 = μ0
- 対立仮説 H1: μ1 ≠ μ0
ですが、これだと「従来の電池の寿命」と「新しい電池の寿命」が同じかどうかを検証する検定になってしまいます。そうではなくて、より寿命が長くなった電池を開発したわけですから、その前提で検定したほうがよさそうです。
この場合、片側検定のほうが適しています。
- 帰無仮説 H0: μ1 = μ0
- 対立仮設 H: μ1 > μ0
「従来の電池の寿命 μ0」と「新しい電池の寿命 μ1」は同じである、と帰無仮説を立てます。対立仮説は、「従来の電池の寿命 μ0」よりも「新しい電池の寿命 μ1」のほうが長い、とします。
検定統計量の分布において、棄却域を分布の片側だけに設定します。棄却域5%であれば、片側に5%を設定します。
このように検定統計量の分布の片側だけをつかって行う検定が片側検定です。
両側検定は、同じかどうかが問題であって、大きいほうに違っても、小さいほうに違っても、違いがないかを検証したいのです。
片側検定は、等しいかどうか異なっているかだけではなくて、理論的に、または経験的に大きくなると考えられることについて、実際に大きくなっているかを検証したいのです。
有意水準の設定
有意水準をα としたら、両側検定の場合は、両側を合わせてα の棄却率とします。
ですので、片側部分だけで見れば、1/2ですから、 α / 2 だということになります。t検定を例にあげて考えてみます。
tの絶対値を|t|、自由度をn-1 とすると、両側検定の場合は、
|t| > tα/2(n-1)
となるかどうかで、検定をします。
※|t|は、プラス、マイナスの方向に関係なく考えたときの値(絶対値)を示しています。
右側の片側検定の場合は、設定している母平均よりも、標本平均が大きくなった場合にだけ帰無仮説を棄却するのですから、棄却域は、
t > tα(n-1)
となります。
また、左側の片側検定の場合は、設定している母平均よりも、標本平均が小さくなった場合にだけ帰無仮説を棄却するのですから、棄却域は、
t < -tα(n-1)
となります。
仮に、0.05(5%)の棄却域を設定するならば、
■両側検定 |t| > t0.025(n-1)
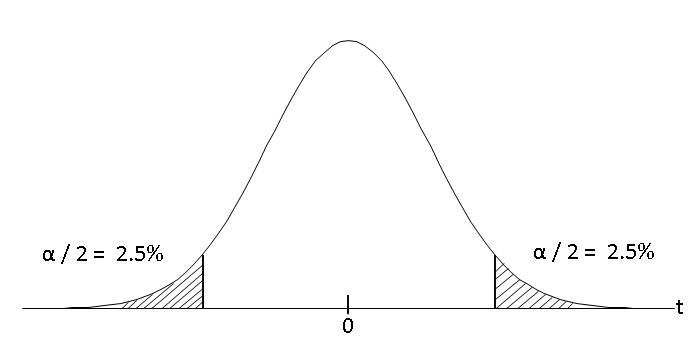
■右片側検定 t > t0.05(n-1)
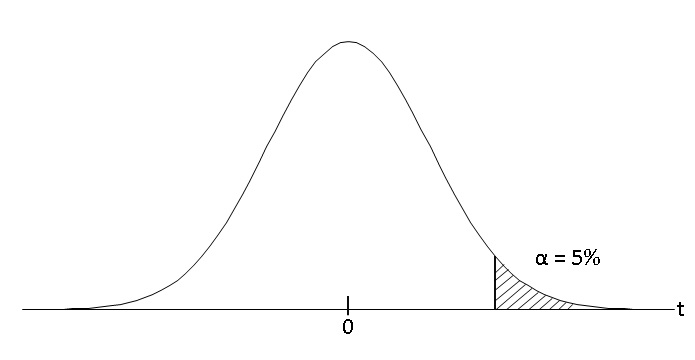
■左片側検定 t < -t0.05(n-1)
このようになります。
仮説を立てる前に片側検定か両側検定のどちらを使うか決めておく
片側だけの棄却域を見ると、片側検定の場合は5%の範囲、両側検定の場合は2.5%の範囲です。両側検定のほうが棄却域の範囲は狭くなり、棄却されにくいです。
両側検定をするのか、片側検定をするのかは、仮説を立てる時点で決めておくことであって、データを集めて分析しているときや検定のための計算を行うときに、やっぱこっちにしようと変えるべきでありません。
ましてや、両側検定で有意にならなかったから、やっぱり片側検定に変えようとやってしまっては、検定結果を操作してしまうことになります。
森田果氏の著書「実証分析入門 データから「因果関係」を読み解く作法」には、
実際には両側検定が使われることがほとんどであり、片側検定が使われることは滅多にない。
そのなかで、あえて片側検定を使うと、読者からは「この分析は、統計的優位性を出したいがために、両側検定でなくて片側検定を使っているのではないか?」と痛くもない腹を探られかねない。
片側検定を使うべききちんとした理由があるならよいが、そうでないのであれば両側検定にして、それでも統計的に優位な結果が出ていれば、読者に疑われずに安心だ。
とあります。
[amazon asin=”4535557934″ kw=”実証分析入門 データから「因果関係」を読み解く作法”]