一様分布とは、確率変数\(x\)の値がいくつであっても、確率密度関数が一定の値をとる分布です。
一様分布には、離散型一様分布と連続型一様分布があります。
“離散”と“連続”の違いは、対象のデータが離散的なデータであるか、連続的なデータであるかの違いです。
離散型一様分布の平均と分散、連続型一様分布の平均と分散について説明していきます。
離散型一様分布とその平均と分散
人数や個数、枚数などのように数えることができるものを離散型データといいます。対象が離散型データである場合、離散型一様分布となります。
確率密度関数の式は、
$$f(x)=\frac{1}{n}$$
です。
これは、$x$がどんな値になろうとも、結果として\(\frac{1}{n}\)となることをあらわしています。
\(x=1\)であっても、\(x=2\)であっても、\(\frac{1}{n}\)となってしまいますね。
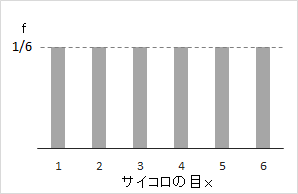
たとえば、サイコロを振って出る目のことを考えてみると、1~6の目がそれぞれ出る確率は同じです。1、2、3、4、5、6のどれであっても、確率は\(\frac{1}{6}\)になります。
確率密度関数の式は、
$$f(x)=\frac{1}{6}\ (x=1,2,3,4,5,6)$$
です。\(x=1,2,3,4,5,6\\)以外の場合は、発生する確率が無くて、\(f(x)=0\)になります。
離散型一様分布の平均、分散、標準偏差
$$μ=\frac{1+2+3+…+n}{n}\\=\frac{1+n}{2}$$
$$\sigma=\sqrt{\sigma^2}$$
サイコロの目の出方について平均、分散、標準偏差を計算してみましょう。
$$平均μ=\frac{1+2+3+4+5+6}{6}\\=\frac{21}{6}\\=3.5$$
$$標準偏差\sigma=\sqrt{2.91667}=1.70783$$
連続型一様分布とその平均と分散
身長や体重などの観測値や時間などは数えることができず、連続的なものです。これを連続型データといいます。対象が連続型データである場合、連続型一様分布となります。
データがとる最小値を\(a\)、最大値を\(b\)とします。
\(x\)は、\(a\)以上、\(b\)以下の値をとる \(a \leq x \leq b\) であり高さは一定です。図のようなグラフであらわせられます。
確率密度関数の式は、
$$f(x)=\frac{1}{(b-a)}$$
となります。
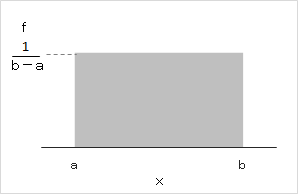
\(f(x)\)は、\(a\)から\(b\)の間で一様に同じ値をとります。図の長方形の面積を1とすれば、長方形の高さは\(\frac{1}{b-a}\)の値になります。
図の長方形を見たときに、底辺が\((b-a)\)であるので、この長方形の図が確率の合計であり、その面積を1とすれば、
$$底辺\times高さ=面積$$
$$(b-a)\times (高さ)=1$$
ですから、
$$ (高さ)=1\div(b-a)$$
となりますよね。
たとえば、\((0\leq x\leq 10)\)のときには、
$$f(x)=\frac{1}{10-0}$$
となります。

連続一様分布の平均、分散、標準偏差
$$μ=\frac{a+b}{2}$$
$$\sigma^2=\frac{(b-a)^2}{12}$$
$$\sigma=\frac{(b-a)}{sqrt{12}}$$
\(x\)が0~10の連続型一様分布の平均、分散、標準偏差を計算してみましょう。
$$平均μ=\frac{0+10}{2}=5$$
$$分散\sigma^2=\frac{(10-0)^2}{12}=\frac{10^2}{12}=\frac{36}{12}=8.33333$$
$$標準偏差\sigma=\sqrt{8.33333}=2.88675$$