ある事象が大小さまざまな大きさで発生することを「分布をする」といいます。それは、データが様々な値をとるということです。
たとえば、成人男性の身長160cmの人もいれば、身長170cmの人もいます。あるいは180cmの人もいます。これを「成人男性の身長は分布する」といった言い方をします。
これらのデータを、階級をつくって区切り、そのなかに入るデータ数(度数)を記載した表を「度数分布表」といいます。
この記事では度数分布表の用語について紹介します。
度数分布表の用語
データの値が並んだだけのものを見ても、そこから何かを見出すのは難しいです。ふつうは表やグラフにして、どのような分布なのかを見ます。そのときに使われるのが度数分布表です。
観測されたデータの最小値から最大値をいくつかに区切って、その区画の中にカウントされたものを「度数」、または「頻度」といいます(frequency)。
度数や頻度のことを記号\(f\)で表し、変数\(x\)の度数を表すときには、\(f(x)\)と表されることもあります。
たとえば、次のようなデータがあるとしましょう。あるオニギリ屋さんで販売されているオニギリの値段です。
種類は30種類あり、安いものはシンプルなオニギリで100円、高いものでは具材をふんだんに使ったオニギリで200円します。
※単位: 円
このデータを度数分布表にまとめてみましょう。
まず100円から20円ごと区画をつくります。データを分類するための区画を「階級」といい、それぞれのデータを当てはまる階級にカウントしていきます。
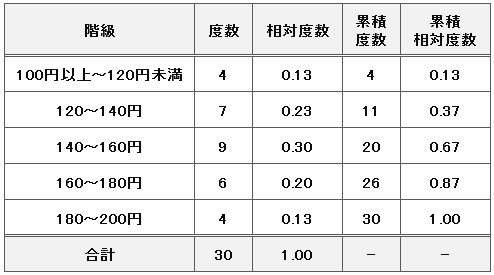
度数には絶対度数と相対度数があります。また足し合わせた度数として累積度数があります。
「絶対度数」とは、観測されたそのままの数のことです。単に度数という場合はこの絶対度数のことを指しています。
「相対度数」とは、全体の中での度数の割合のことです。上記表で100円~120円未満の飲み物の相対度数は、30品中、4品ありますから0.13となります。
「累積度数」とは、下の階級から度数を足し合わせていったものです。
120~140円の階級では、100~120円の階級の度数が4、120~140円の階級の度数は7、ですから、120~140円の階級の累積度数は11 になります。
「累積相対度数」とは、全体の中での累積度数の割合のことです。
120~140円の階級の累積度数は11 で、全体の度数は30 ですから、11÷30 で累積相対度数は0.37 となります。階級が上になるにつれて1.00 に近づきます。180~200円の階級の累積相対度数は1.00 になります。
ヒストグラム
度数分布表にまとめられたデータの分布状況をグラフにしたものを「ヒストグラム」といいます。
エクセルのグラフ作成機能で、棒グラフを選択し、度数のデータを指定すれば、ヒストグラムを作成することができます。
(histogram:柱状分布)
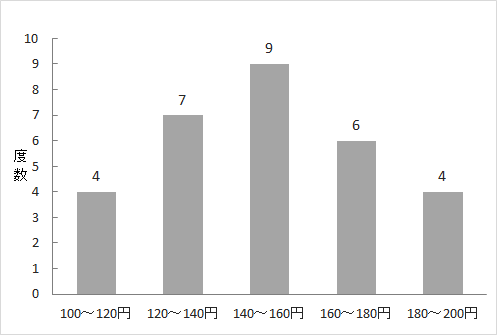
分布をヒストグラムで表すとこのようになります。
ヒストグラムの作り方についてはこちらの記事で詳しく解説をしています。
エクセルで度数分布表を作るには、FREQUENCY 関数がつかえます。
FREQUENCY 関数で度数を計算して、度数分布表としてまとめ、それを表にすればヒストグラムになります。下記の記事を参考にしてください。