条件付き確率の問題　モンティ・ホール問題

あなたはこんなゲームに参加をしました。そこには「左のドア」・「真ん中のドア」・「右のドア」の3つのドアが並んでいます。ひとりのゲーム司会者がゲームの説明をしてくれます。

「この3つのドアのうち、ひとつは当たりのドア、残りのふたつはハズレのドアです。当たりのドアを開ければあなたの勝ち、ハズレのドアを開ければあなたの負け、となるゲームです。」

あなたは、どのドアが当たりなのかはもちろん知りません。正解を知っているのは司会者だけです。直感で「左のドア」を選びました。ここで当たりのドアを選ぶ確率は、1/3です。まだドアは開けていません。選んだだけの状況です。

すると、ゲーム司会者が「真ん中」のドアを開けてハズレであることを示しました。

そして、司会者はこのようなことを言い出しました

「こちらの真ん中のドアは不正解でした。左のドアか右のドアが正解なわけですが、選ぶドアを左から、右のドアに変更することもできます。もちろん変更しないで左のドアのままでも大丈夫です。どうしますか？」

残っているドアは、最初にあなたが選択した「左のドア」、そして司会者が残した「右のドア」です。ここで、あなたはドアを変更すべきなのかどうか。

直観としては、どちらのドアを選んでも、変わりはないように思いますよね。正解が当たる確率は「左のドア」も「右のドア」も変わらず1/2のように思いますが…。

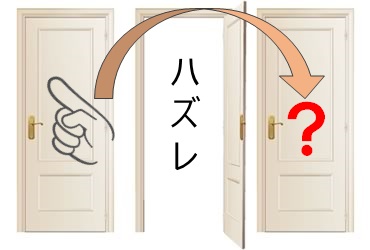
ここでどうすべきかというと、実は、最初に選んだ「左のドア」から「右のドア」へと変更したほうが当たりのドアを開けられる確率が高まります。

実際には、「左のドア」Ａが当たる確率は1/3で、「右のドア」が当たる確率は2/3となるのです。最初に選んだドアから変更したほうが、当たりとなる確率が2倍になります。それはなぜか。

司会者が「真ん中のドア」を開ける前の段階では、左、真ん中、右のドアいずれも当たる確率は1/3でした。あなたは「左のドア」を選んだわけですが、それが当たるのは1/3の確率。残りの「真ん中のドア」と「右のドア」が当たる確率は2/3になります。

司会者が「真ん中のドア」が正解でないことを示しました。もともと「真ん中のドア」と「右のドア」で2/3の確率であったところ、「真ん中のドア」は正解ではないとわかったのですから、「右のドア」が当たる確率がそのまま2/3となるのです。

直観で正しいと思うことと、実際に正しいことに、ズレが生じる問題ですね。

トランプで試してみる

これは実験してみると体感することができます。実際にドアを置いてやってみたいですが、自宅には3つの並んだドアはありませんので、トランプでやってみることにしました。

誰かもうひとりと一緒に行っていきます。3枚のトランプを用意しました。ジョーカー2枚とエース1枚です。ジョーカーはハズレ、エースは当たり、とします。

相手に3枚のトランプを並べて置いてもらい、そのうちの1枚を選びます。それがエースであれば正解です。

上記のドアの問題と同じように、私がトランプを1枚、指さして選んだあとに、カードが
わかっている相手に、のこり2枚のうちのジョーカーをめくってもらいます。

そこで、カードを変えたほうが当たりやすいか、それとも変えないほうが当たりやすいか、それをカウントしてみました。これを50回繰り返して、選ぶカードを変更しないのと、変更するのとで、どちらが当たるのかを数えていくと、次のような結果となりました。

最初に選んだカードから

• すべて変更しないとしたら・・・15回当たり
• すべて変更するとしたら・・・35回当たり

変更をしたほうが、おおよそ2倍くらい当たりが多くなりました。

割合は1/3 と、2/3 にはなっていませんが、さらに繰り返していけば大数の法則に従って、その割合に収束していくと思われます。

さきほどのドアの問題でいえば、自分が最初に選んだドアをそのまま選ぶと50回中、15回当たり、司会者が残したドアを選ぶのを50回やると35回当たることになります。

やって感じたのは、選んだカードを変えないとすると、最初に選んだカードが当たるかどうかだけの問題だということです。3枚のうち最初に選んだカードが当たっていれば、当たり。確率は1/3で、そこは確定していますね。

ドアを3枚から1万枚へ増やすと

思考実験としてわかりやすくするには、10000枚のドアがあると考えることです。

ずらっと左から右へと順番に番号が振られた10000枚のドアが並んでいて、どこかに当たりがあります。

あなたは一番左の1枚目のドアを選びました。そしたら司会者が2枚目から9999枚目までのドアをすべて開けてハズレであることを示しました。残ったのは10000枚目のドア1枚だけです。

こう考えると、10000枚目のドアに正解がある確率が高いように感じ、選ぶドアを変更したくなるかと思います。

この問題は、アメリカの番組で実際につかわれたもので、モンティ・ホール問題と呼ばれてす。番組の司会者の名前がとってつけられて、モンティ・ホール問題と名付けられたのです。