ベルヌーイ試行と二項分布について、また、その違い、関係性についてを書きました。
ベルヌーイ試行
1回の試行で、2種類のどちらかの事象しか起こらない試行をベルヌーイ試行といいます。
片方の事象が発生する確率を\(p\)、とすれば、もう片方は \(1-p\) です。これが、同じ条件で独立して繰り返されることです。
たとえば、コイン投げをして、表が出るか裏が出るかについてを考えてみましょう。
コイン投げを行ったときに起こる結果はこの2つしかありません。表が出る確率、裏が出る確率は、それぞれ\(\frac{1}{2}\)ですね。
またその他には、YesかNoか、男か女か、良品か不良品か、といった具合で、二つに一つの結果となるものです。
二項分布
二項分布とは
コイン投げをして、表が出るか裏が出るかを見るのは、ベルヌーイ試行です。ベルヌーイ試行であるコイン投げを、10回行ったうち、表が出る回数が従う確率分布が、二項分布となります。
10回中、表が出る回数は0~10回となります。
表が出るか裏が出るかは、1/2の確率なのですから、10回コインを投げたら、だいたい半分の5回付近になることが多そうな気はしますね。10回とも表が出ることや逆に0回ということは、ひょっとしたらあるかもしれませんが、確率はものすごく小さそうです。
ためしに10回コインを投げてみる、何回表が出たかを記録する。
再度、10回コインを投げてみる、何回表が出たかを記録する。
なんども繰り返していくと、表が出た回数は5回であったり、7回であったり、4回であったり、様々な回数になるでしょう。
それを繰り返していけば、分布がつくられます。
成功するか失敗するか、一定の確率があるベルヌーイ試行を、$n$ 回行ったときに何回成功するのかを示した分布が、二項分布です。
成功確率\(p\) のベルヌーイ試行を\(n\) 回行うときに、ちょうど\(x\) 回成功する確率は次の式で計算できます。
$$f(x)=_n C_x \times p^x \times(1-p)^{n-x}$$
\(_n C_x\) は、\(n\) 個のなかから\(x\) 個を取るときの組み合わせの数をあらわしています。
10回のコイン投げで0~10回、表が出る確率は?
例として、10回のコイン投げをとりあげます。
表が出ることが「成功」であるとして、0~10回それぞれ成功する(表が出る)確率を順番に見ていきましょう。
コイン投げで表が出る確率$p$ は0.5です。まず、10回コイン投げをして、0回成功する確率は、次のように計算します。
$$f(0)=_{10} C_0 \times 0.5^0 \times(1-0.5)^{10-0}$$
$$=1\times 1\times 0.000976$$
$$=0.000976$$
10回コイン投げをして、0回成功する確率は、0.000976です。ちなみに、$f(0)$はコイン投げをして表が出るのが0回になる確率をあらわしています。表が出るのが5回になる確率なら、$f(5)$です。
10回コイン投げをして、1回成功する確率は、
$$f(1)=_{10} C_1 \times 0.5^1 \times(1-0.5)^{10-1}$$
$$=10\times 0.5\times 0.00195$$
$$=0.009766$$
10回コイン投げをして、2回成功する確率は、
$$f(2)=_{10} C_2 \times 0.5^2 \times(1-0.5)^{10-2}$$
$$=45\times 0.25\times 0.00390$$
$$=0.04395$$
このような具合で、計算していくと次のようにまとまります。
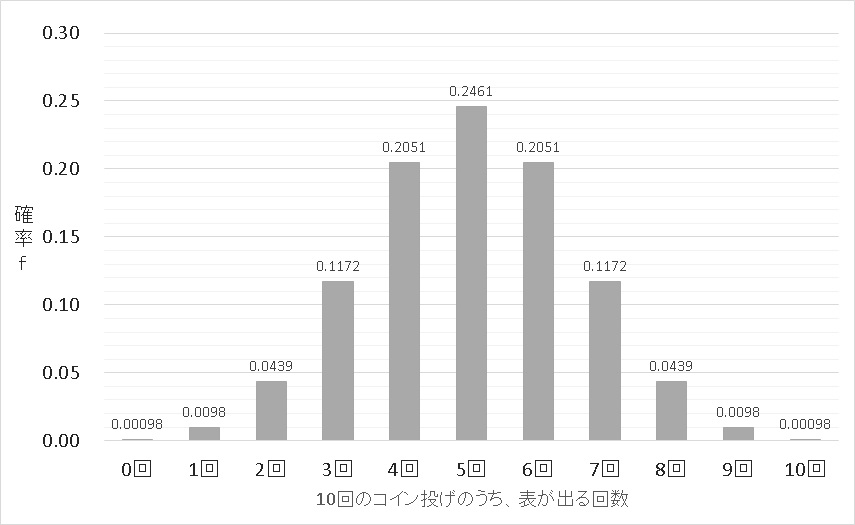
$$f(0)=_{10} C_0 \times 0.5^0 \times(1-0.5)^{10-0}=0.00098$$
$$f(1)=_{10} C_1 \times 0.5^1 \times(1-0.5)^{10-1}=0.0098$$
$$f(2)=_{10} C_2 \times 0.5^2 \times(1-0.5)^{10-2}=0.0439$$
$$f(3)=_{10} C_3 \times 0.5^3 \times(1-0.5)^{10-3}=0.1172$$
$$f(4)=_{10} C_4 \times 0.5^4 \times(1-0.5)^{10-4}=0.2051$$
$$f(5)=_{10} C_5 \times 0.5^5 \times(1-0.5)^{10-5}=0.2461$$
$$f(6)=_{10} C_6 \times 0.5^6 \times(1-0.5)^{10-6}=0.2051$$
$$f(7)=_{10} C_7 \times 0.5^7 \times(1-0.5)^{10-7}=0.1172$$
$$f(8)=_{10} C_8 \times 0.5^8 \times(1-0.5)^{10-8}=0.0439$$
$$f(9)=_{10} C_9 \times 0.5^9 \times(1-0.5)^{10-9}=0.0098$$
$$f(10)=_{10} C_{10} \times 0.5^{10} \times(1-0.5)^{10-10}=0.00098$$
当然、表が出る回数が0~10回のそれぞれの確率を足し合わせると、1 となります。
二項分布は英語で、binomial distributionといいますから、\(Bi(n,p)\)とあらわされます。\(n\) は試行回数、\(p\) は成功確率です。
二項分布に従う\(X\) の期待値と分散は、次のとおりです。
期待値 \(E(X)=np\)
分散 \(V(X)=np(1-p)\)
\(1-p\) を\(q\) とあらわすことも多いです。そうすると、
分散 \(V(X)=npq\)
となります。
10回コインを投げて、0.5の成功確率である表が\(x\) 回出る確率分布 \(Bi(10, 0.5)\)に従う\(X\) の期待値と分散は、
\(E(X)=10\times0.5\\=5\)
\(V(X)=10\times0.5\times(1-0.5)\\=2.5\)
です。10回コインを投げたときの期待値は、5回となりました。
ベルヌーイ試行と二項分布の違いと関係性
ベルヌーイ試行は、ある確率の2種類の事象が起こる試行のことです。
二項分布は、ベルヌーイ試行を\(n\) 回行って、そのうち成功する回数の分布のことを指しています。
コメント
> 二項分布のことをベルヌーイ分布とも言います。
これは間違いではないでしょうか。
ベルヌーイ分布は、二項分布で試行回数が1の場合の分布を意味する名称だと思います。