散布図とはそもそもどんな図なのか。どのように作られるのか。また、正の相関関係・負の相関関係は、散布図ではどのように見えるのか…といったことについて書きました。
散布図とは
散布図とは、2つの変数の間の関係を見るために、縦軸と横軸に目盛りを設けてデータを打点(プロット)した図です。
2つの変数にはどのような関係があるか、一方が増えるともう一方はどのように変化するのか、一方が減るともう一方はどのように変化するのか、散布図から読みとることができます。
たとえば、
- ヒトの身長と体重
- ヒトの親と子の身長
- 数学テストの得点と英語テストの得点
などです。ヒトは身長が高いほど体重も重くなる傾向があるでしょう。親の背が高ければ遺伝的に子の背も高くなる傾向にあるでしょう。
ここに10人の国語のテスト、英語のテストの結果があります。
・10人の国語の得点、英語の得点
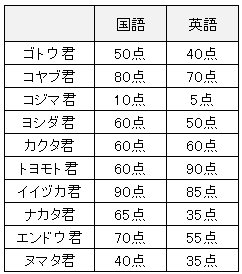
散布図の書き方
この2つの科目のテストの得点に、 どのような関係があるのか散布図書いて、見てみましょう。
散布図の横軸を国語の得点とし、縦軸を英語の得点とします。その2つが交わる箇所に点を打ちます。
これを10人分の得点を打点すれば、散布図が完成します。
まずは、ゴトウ君の得点を打点してみましょう。国語は50点、英語は40点です。
※点を打つことをプロットと言ったりもします。
☆ゴトウ君の点数を打点(プロット)
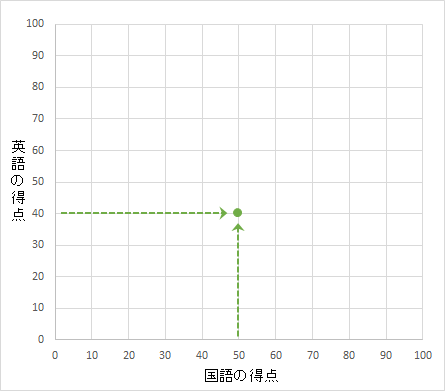
次にコヤブ君の国語得点80点と英語の得点70点も打点します。
☆コヤブ君の点数を打点(プロット)
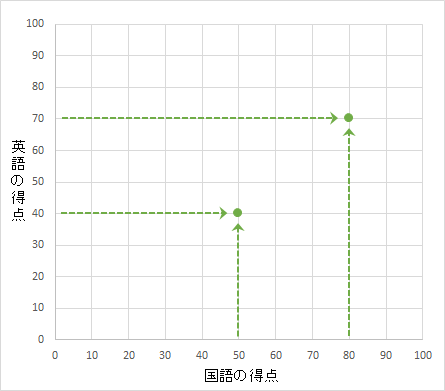
この作業を繰り返し、10人の国語の得点と英語の得点を打点していくと、下のような散布図が完成します。
☆散布図 完成
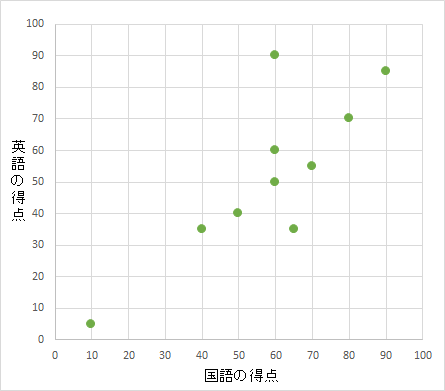
散布図を見ると、打点が右肩上がりになっており、国語の得点が高いほど、英語の得点も高くなる関係が見られます。
このように2つの変数が連動する関係のことを相関関係といい、一方の値が大きければ、もう一方の値も大きくなる傾向があることを、
「xとyの間に正の相関がある」
といいます。
逆に一方の値が大きくなると、もう一方の値が小さくなる傾向があれば、
「xとyの間に負の相関がある」
といいます。
相関関係の正・負、また強弱の言い表し方
2つの変数を、一方をxとし、もう一方をyとしたら、上記した国語の得点と英語の得点のように、正の相関もあれば、負の相関もありますし、その程度にもいろいろあります。
相関関係の正・負、また強弱について下記のように言い表します。
| (1) | xが大きくなれば、yも直線的に大きくなる場合 | xとyの間に強い正の相関がある |
| (2) | xが大きくなれば、yも大きくなる傾向がある場 | xとyの間に正の相関があ |
| (3) | xが大きくなっても、yが大きくなるわけではない場合(散布図上にバラバラに打点されている) | 相関が無い |
| (4) | xが大きくなれば、yが小さくなる傾向がある場合 | xとyの間に負の相関がある |
| (5) | xが大きくなれば、yが直線的に小さくなる場合 | xとyの間に強い負の相関がある |
散布図では、どのように打点がされるのかも合わせて見てください。
散布図の見方。正の相関や負の相関は、散布図上ではどのように見えるか
これらを散布図で見ると、次のような打点のされ方となります。
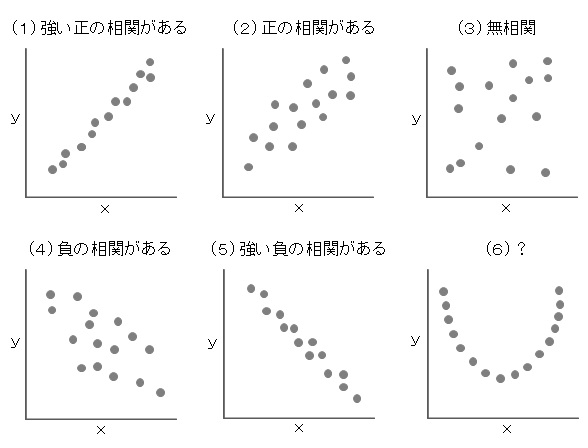
どのくらい相関関係があるのかを示す数値として、相関係数があります。 相関係数は、-1 ~ 0 ~ +1の間の値をとります。正の相関があるとプラスの値、負の相関があると相関係数はマイナスになります。
正の相関
正の相関が強いほど相関係数は+1に近づき、散布図上では(1)のような図になります。右肩上がりに打点されていますね。
相関係数=1.0の場合には、打点が完全に直線になります。(1)の図は完全な直線ではないですが、それに近くなっており、相関係数=0.9程です。1.0 に近いので強い正の相関があるといえます。
ところで、先ほど散布図を書いた10人のテスト結果で、国語の得点と英語の得点の相関係数は、0.81です。
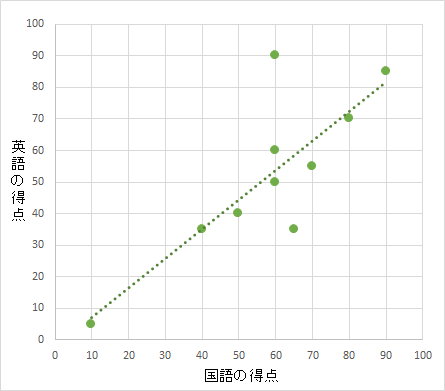
相関係数は0.81はなかなかの強い相関であるといえます。
※ただし10人だけのデータで精度が高くないですから、実際に活用する場合にはもっとたくさんデータ(30個以上)を集めた方がよいです。
無相関
正の相関が弱くなると相関係数が0 に近づいていき、0 になると全く相関が無い状態、つまり無相関で、図(3)のような散布図になります。
■意味のある無相関
図(6)のような散布図では相関係数は0 に近くなります。相関係数としては無相関ではありますが、このような打点にはなんらかの意味があるのではないかと思われます。
打点が直線的になっておらず相関係数では相関がないと判断できても、2つの変数の間にはなにか関係性があることはありえます。
負の相関
xが小さくなると、yも小さくなるという負の相関では、相関係数はマイナスの値をとり、図(4)のような散布図となります。
さらに負の相関が強くなると、図(5)のように直線に近くなり、打点が完全な直線になると相関係数が-1 となります。
散布図上での打点の傾き角度は、相関の強さに関係しない
ちなみに、散布図上での打点の集まりの傾き・角度は、相関の強さ・弱さに関係がありません。
バラつきが小さく直線的になっているかなっていないかが、相関の強弱です。
ためしに、下図のように縦軸の目盛りを200までにしてみたり、
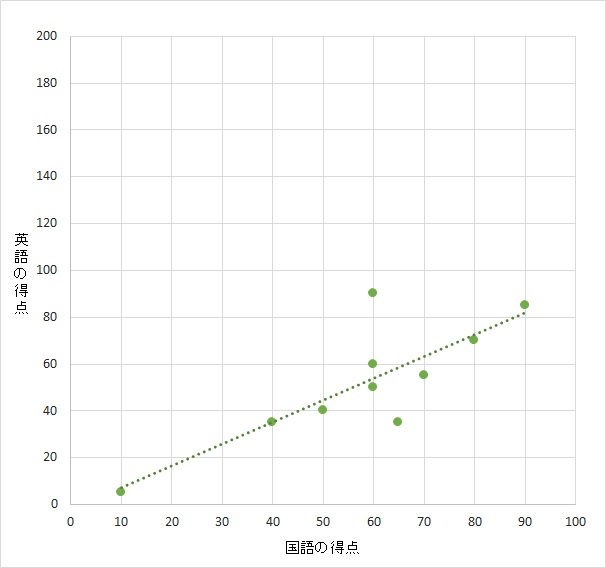
グラフを正方形から長方形に変えるなどすれば、打点上に引いた線の傾きは簡単に変わります。
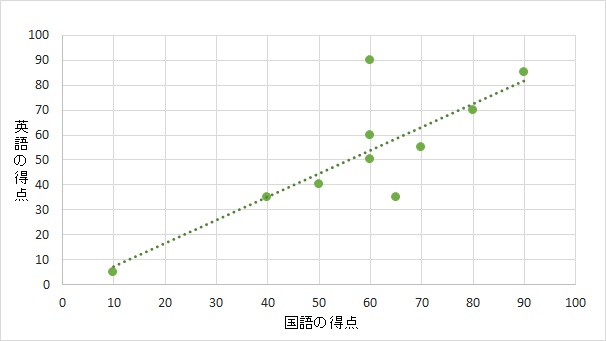
傾きは変わったとしても、当然ながら得点と相関係数は変わっていません。傾きと相関係数は関係がないことがわかります。