検定の考え方は、最初のうちはわかりづらく感じるかもしれませんが、実は、私たちは普段の生活でもこの考え方を使っています。
職場への出社時間が遅れている二人を心配すべきかどうか、検定の考え方を説明します。
きっちり時間を守る人、時間にルーズな人
ここに、きっちりと時間を守る同僚のAさん、時間にルーズなBさんがいます。
Aさんは、平均的には8:45に職場に到着します。早いときには8:40、遅くとも8:50には到着する几帳面な人です。
もうひとりのBさんは、ちょっとルーズなところがあり、平均的にはギリギリで9:00に着、早くから用事があるときには8:40に出社することもありますが、遅いときは9:20になることもあり、しょっちゅう遅刻もしています。
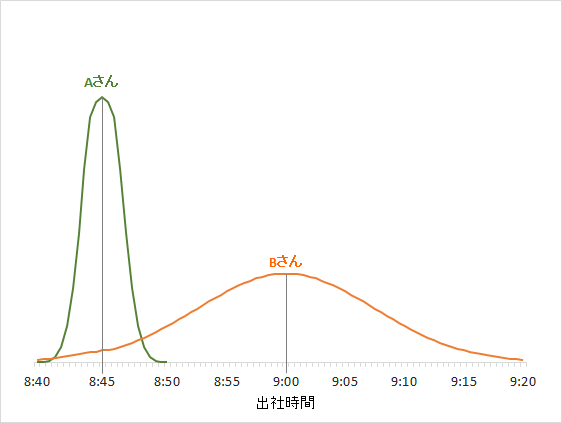
この2人の出社時間をグラフにすると下記のようになります。
Aさんは、8:45を中心として、多少の前後はあるけれども大きくズレることがありません。毎日ぴったり同じ時間に家を出ているようです。
Bさんは、平均的には9:00出社ですが、早く来る日もあれば、9:00を過ぎてしまうこともよくあります。
始業時間の9時を過ぎてもやって来ない二人をどう思うか?
二人が9:10になっても職場にやって来なかった時のことを考えてみましょう。
Aさんが遅れてきた場合の周囲の反応は、こうです。
「いつもきっちりと8:45前後は到着しているのに、おかしい。何かあったのではないか?事故にでもあったのではないか?」と上司や同僚が心配を始め、連絡をとってみたりするでしょう。
これは、「ふつうではない。異常である。」と判断したことになります。
一方、Bさんが遅れてきたときは、こうです。
「いつも9:00ギリギリにくることが多いけれども、9:10以降になることもある。いつものように遅れているのだろう」と上司や同僚は考えます。そのうち来るだろうと思って何も行動しません。
これは、「ふつうことである。異常ではない。」と判断したことになります。
9:30になったらどうでしょうか。Aさんの場合は、同僚たちが絶対なにかあったに違いないという気持ちを強め、Bさんの場合は、何かあったのかもしれないと少し思うくらいでしょう。
日常生活でも検定に近い考え方で判断をしている
この二人に対する心配度合いの違いは、出社時間の平均値と標準偏差で説明できます。
出社時間のする平均と、ばらつきがどのくらいなのかによって、遅れてきた場合の判断が変わってきます。
Aさんは、平均値8:45で、標準偏差の値も小さく出社時間のばらつきが小さいので、9:00を過ぎる確率は小さく、
Bさんは、平均値が9:00であり、標準偏差の値も大きく、9:00を過ぎる確率は大きいです。
職場の人たちは、「Aさんが遅れるとは、おかしい。なにか事故にでもあったのでは?」と判断をするのですが、このときのふつうの考え方と、仮説検定的な考え方を比較してみましょう。
| ふつうの考え方 Aさんが9:10になっても出社してこない。いつもは8:45に出社していて、遅刻して9:00を過ぎることはまずない。それが起こるのはめったにないだろう。ひょっとして事故にでもあったのでは? |
| 仮説検定的な考え方 Aさんが9:10になっても出社してこない。 「ふつうのことである」という仮説H0が正しいとしたら、出社時間が9:10を過ぎる確率はかなり小さいである。 有意水準5%以下の小さな確率になるので、仮説H0は棄却し、このできごとは、ふつうのことであるとはいえない。出勤中に事故にあったなど、何か異常が起きたと判断する。 |
どうでしょう。似ていると思いませんか?
普段の考え方と仮説検定的な考え方を比較すると、後者はちょっと堅苦しく難しいだけで、同じことを言っているのがわかります。
これはいろんなことに当てはまりますね。
「風邪ひいたかも…いや、まだ大丈夫だ。いや、風邪に違いない。」とか、「あの人は私のこと好きなのかも…いや、違う。いや好きに違いない。」など、いろいろな場面でこれをやっています。
普段、ものごとを判定するときに使っているときに、統計学の用語をつかい、確率的なことを計算しつつ判定をすれば、そのまま検定してることになりそうです。