余事象とは、ある事象が起きない確率のことです。
ある事象を確率の計算をするときに、ふつうに計算するよりも余事象をつかうと早く計算できることがあります。
この記事では、余事象の意味や計算方法について紹介します。
余事象の意味
Aの事象に対して、Aではない事象を「余事象」といいます。
A という事象があったら、A 以外のすべてのできごとが余事象ですね。
余事象の記号とベン図
余事象の記号は「AC」です。ベンズ図とは標本空間の概念を図であわらしたもので、次のような図になります。
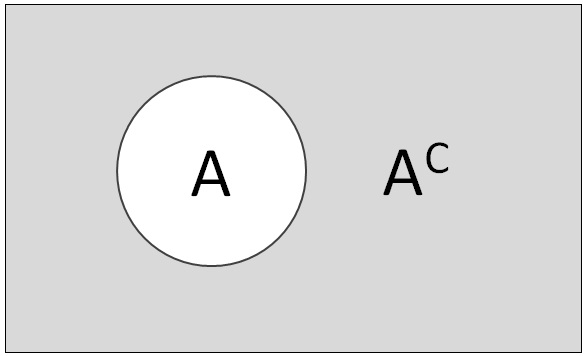
事象A以外の部分が、余事象「AC」です。
余事象はいつ使うのか、どのように役立つか
Aという事象があったとき、それが発生する確率をふつうに計算することが難しくても、余事象をつかって逆から計算すると簡単に計算できることがあります。
いくつものパターンを計算しなくてはならないときがそうです。確率を計算するのは、複雑で難しくなります。
そのときに、“余事象”(A事象が起こらないこと)を計算するのは簡単であるならば、Aの“余事象”を計算して、100%から“余事象”の確率をマイナスすれば、その答えがA事象の確率です。
簡単に計算できてしまいます。
野球の打席を例にとって、余事象がどのように役立つか、また計算方法について説明していきます。
野球の試合が始まってまず打席に入る1番打者、2番打者、3番打者たちは、いいバッターが揃っていますよね。
試合開始直後の1番打者、2番打者、3番打者がヒットを打ってくれるとチームは勢いづきますし、ファンのテンションも上がります。 逆に開始早々3者連続で凡退してしまうと、ファンもがっくりしてしまいます。
応援しているチームの1番、2番、3番バッターがそれぞれ打率3割だとしましょう。
3者が連続で凡退せずに、3人のうち少なくとも1人以上がヒットやホームランを打って塁に出てくれる確率はどのくらいなのでしょうか。
デッドボールとか振り逃げとかいろいろな場合があるかと思いますが、ここでは、ヒットを打って塁に出るか、アウトになるかだけで考えてみます。3人の3割という打率もヒットを打つ打率として考えてみます。
「3人のうち少なくとも1人がヒットを打つ確率」を素直に計算していくには、1番打者だけがヒットを打つ確率、2番打者だけがヒットを打つ確率、3番打者だけがヒットを打つ確率、1番と2番打者の2人がヒットを打つ確率、3人ともヒットを打つ確率・・・
などなどすべての場合を計算しないといけないので大変。
ふつうに計算していくと手間がかかります。
こういったときは、求めたい確率の反対、つまりそうでない確率(余事象の確率)を考えると、簡単に計算できることがあります。
この野球の話だと、「少なくとも1人がヒットを打つこと」の余事象は、3者が連続でアウトになることです。この余事象であれば簡単に計算できます。
3者が連続アウトになる以外のことの確率が、=「少なくとも1人がヒットを打つ確率」なのですから、まず3者が連続でアウトになる確率を計算し、100%からその確率をマイナスすれば、少なくとも1人がヒットを打つ確率を計算できるわけです。
余事象の計算方法(少なくとも1人がヒットを打つ確率)
ここでは、ヒットを打って塁に出るか、アウトになってしまうか、だけで考えてみます。
「少なくとも1人がヒットを打つ事象」は、「3人全員がアウトにならない事象」とイコールですから、「3人全員がアウトになる事象」の余事象となります。
「少なくとも1人がヒットを打つ」は、「3人全員がアウトになる確率」を計算して、1からそれを引けばいいのです。
1-(3人全員がアウトの確率)=(少なくとも1人がヒットを打つ確率」
となります。
「3人全員がアウトになる確率」は、それぞれの1人ずつのヒットを打たない確率を掛け算すれば計算できます。3人のヒットを打つ打率は3割です。この裏返しで、7割は凡打でアウトとなるのですから、
$$0.7\times0.7\times0.7=0.343$$
34.3%の確率で、3人ともアウトになってしまいます。
この余事象は、
$$100%-34.3%=65.7%$$
3人のうち1人以上がヒットを打つ確率は、65.7%です。
応援しているチームの初回の攻撃では、34.3%の確率で3人連続で凡退し、65.7%の確率は誰かしらがヒットを打ちます。3試合に1試合は盛り上がりにかけてしまいますが、3試合に2試合は初回からヒットが出るので盛りあがるというわけです。